El dominio se divide en dos trozos
x€[0, 1]; y€[-x+2, -x+1]
x€[1, 2]; y€[0, -x+2]
Luego hay que integrar la función en esos dos trozos.
¡ Pues ya me dirás como se integra cos[(x-y)/(x+y)]dy !
Porque los programas se quedan bloqueados y a mano tras hacer el cambio
z = (x-y) /(x+y)
Queda la integral 2ycos(z)dz/(1-z)^2 que tampoco pueden integrar.
A lo mejor es que he llegado también al límite de mis conocimientos y se necesite alguna teoría extra para hacer esa integral.
--------------------------
d)
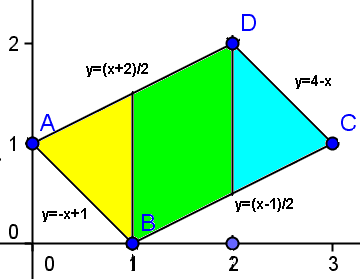
Hay tres intervalos de integración
x€[0,1]; y€[-x+1, (x+2)/2]
x€[1,2]; y€[(x-1)/2, (x+2)/2]
x€[2,3]; y€[(x-1)/2, 4-x]
Y la integral, está vez es polinómica
$ (x+y)^5 dy = (1/6)(x+y)^6
Pero es un lio cuando sustituyamos ahora y por los límites. Desde qluego que saldréis bien formados si hacéis todos estos problemas.
En el primer intervalo vale 8517/896
En el segundo vale 15405/64
Y en el tercero 387333/ 896
La suma = (8517 + 14 · 15405 + 387333) / 896 = 611520 / 896 =
1365/2Bueno, he procurado hacerlo bien, pero puede que haya tenido algún error, no des la solución como segura del todo.
Y ya te digo: ¡Vaya ejercicios! El que no es imposible lo hacen requete pesado.
Espero que te sirva de algo lo que estoy haciendo. De momento no ha habido ninguno sencillo que haya tenido ánimo de resolver por completo.





