Regresión Exponencial y coeficientes de correlación
Te pregunté hace ya bastante tiempo y tu respuesta me fue de gran ayuda, a ver si de nuevo me puedes echar un capote.
He hecho una regresión exponencial (la típica de y=a*exp(bx) ) linealizando mediante logaritmos. He ajustado mis valores y a la hora de buscar el coeficiente de correlación he usado la fórmula de r= COVxy/sqrt(VARx*VARy).
Mi pregunta es si esa formula se puede usar tanto para la ecuación linealizada como para la ecuación deshecho el cambio. El problema es que para la ec. Linealizada el ajuste es de 0.72 y para la no linealizada es de 0.48. Me resulta raro que el ajuste sea "bueno" linealizado y sin el cambio malo. ¿No debería tener la misma bondad el ajuste? ¿Quizás para ver la correlación entre las variables en la forma exponencial haya que utilizar otro método?
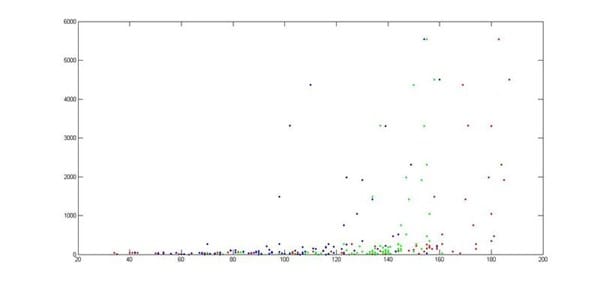
Te agradezco cualquier tipo de ayuda complementaria, estoy ajustando datos de campo de turbidez a valores de intensidad de RGB y se me quedan la nube de puntos con la siguiente forma (serían tres curvas de ajuste para rojo/verde/azul claro): 
1 respuesta
El índice de correlación de dos variables es una característica propia de las dos variables, es independiente de que hagas una regresión lineal o exponencial de las mismas.
Si te da un valor distinto es porque no estás calculando el índice de regresión de las mismas variables.
Si lo calculas de la ecuación linealizada estas calculando el índice de correlación entre X y ln(Y), mientra que de la otra forma lo calculas de X e Y. Son dos índices de correlación de variables distintas y por tanto pueden ser distintos. Además la variable ln(Y) no se parece mucho a Y poro que el índice puede ser muy dispar. Y sobre la bondad no hay normas absolutas. Un indice de correlación pequeño pero calculado con muchos puntos puede corresponder a variables más incorreladas que uno alto calculado con pocos puntos.
