Tomando en cuenta las reglas de derivaciones, solucionar:
Resolver los siguientes problemas con derivadas, con ayuda de las reglas de derivaciones:
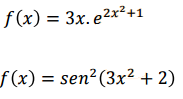
2 Respuestas
Respuesta de ricardo victorio
1
Respuesta de Valero Angel Serrano Mercadal
1

