Problema asociado a la contracción de la longitud
Me pueden explicar el procedimiento para desarrollar este problema
Cuando está en reposo, una nave espacial tiene la forma de un triángulo isósceles cuyos dos lados iguales tienen una longitud 2L y cuya base tiene una longitud de L . Si esta nave vuela y pasa junto a un observador con una velocidad relativa de 0,5 C dirigida a lo largo de su base, ¿cuáles son las longitudes de los tres lados de la nave, de acuerdo con el observador?
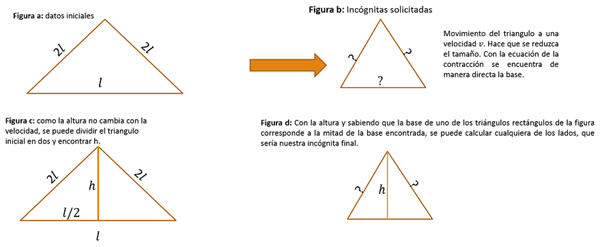
Este problema está asociado a la contracción de la longitud, donde se dan los datos de la figura a y la velocidad con la que se movería el triángulo, por lo cual:
Primero: Se solicita la base y los lados del triángulo isósceles (incógnitas del problema – Figura b), por lo cual se recomienda lo siguiente:
Segundo: calcular la base del triángulo de la figura b) a partir de la velocidad suministrada y longitudes iniciales y aplicando la contracción de la longitud, para ello, se debe identificar cual es la incógnita si L o Lp.
Tercero: como la altura no cambia para ninguno de los triángulos (ya sea en movimiento o no) se procede a calcular la altura mostrada en la figura c).
Cuarto: Con la altura y conociendo la base del triángulo rectángulo que está en movimiento (ver figura d) se procede a aplicar geometría para encontrar la incógnita de los dos lados solicitada.
1 respuesta
Cuando la figura que te dicen ( triangulo isósceles)se translada paralelamente a su base a velocidades grandes, sus dimensiones se modifican como consecuencia de las Tranformaciones de Lorentz referidas a dos sistemas inerciales que se mueven uniformemente uno respecto del otro.
Aquí se modificaran solamente las longitudes paralelas al sentido del movimiento. Como la altura de triangulo es perpendicular al sentido del movimiento, se mantendrá invariable vista desde un observador situado en el sistema fijo. No ocurre lo mismo con las longitudes de base y lados.
Long. de la base referida al sistema en reposo = L
Longitud de la base moviendose a velocidades muy grandes ( 0.5 c) = Lo (1- v^2/c^2)^1/2 segun transformacion de Lorentz...
= L ( 1 - 0.5^2)^1/2 = 0.866 L .........................o sea la base se ha acortado un 13%...............
Los lados del triangulo ( iguales cada uno a 2L) modifican su longitud porque su componente horizontal cambia, mientras que su componente vertical no...
Componente horizontal del lado = L/2 ..............que se modificaria a L/2 (1- v^2/c^2)^1/2 =
= 0.866 L/2 cada uno.
Componente vertical = altura del triangulo isosceles = (4L^2 - L^2/4 )^1/2 L = 1.9365 L
Luego el triangulo original de base L y lados 2L se vería como otro triangulo igualmente isósceles de base 0.866L ... y lados de longitud ( 0.433^2 + 1.9365^2)^1/2 L = 1.9843 L
