Anónimo
Potencia máxima disipada de una resistencia
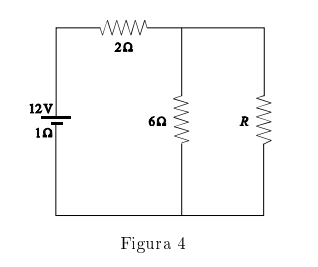
a) Hallar el valor de R para que la potencia disipada en ella sea máxima.
b) El valor de R para que la potencia disipada sea 6 W
2 respuestas
Para resolverlo debes separar la resistencia R sola. Y hallar el equivalente Thevenim de todo el circuito restante. No lo podes plantear de otra forma.
Llegarias al esquema:
VTh en serie con RTh en serie con R.
a) Equivalente Thevenim del circuito que te queda a la izquierda de R:
RTh = 6//3 = 18/9 = 2 ohms.
VTh = 6 x ( 12/9) = 8 Volts.
Potencia máxima transferida= potencia transferida pára R= RTh .........
Pmax. = VTh^2 / 4 RTh = 64/ 4. 2 = 8 Watts.
b) R para que la potencia disipada sea 6 W.
Volves al circuito completo con VTh, RTh y R todo en serie tenes;
PotenCIA( R) = I^2 R = {VTh^2 / ( RTh + R)^2} R
6 Watts = { 64 / (2 + R)^2} R ..............y despejas el R que te cumple con la condicion pedida.
No voy ha hacer tus tareas escolares.
Solo te diré que para encontrar la solución a la primera cuestión tienes que aplicar la ley de máxima transferencia de energía que viene a decir que una resistencia en serie con un generador producirá la máxima potencia posible cuando su valor sea igual a la resistencia interna del generador.
En este caso asumiremos que la resistencia interna del generador sera 1 ohmio más los 2 ohmios de la resistencia en serie lo cual nos da una resistencia equivalente de 3 ohmios. Sabiendo eso tenemos que encontrar la resistencia serie equivalente de las dos en paralelo para que su valor sea de 3 ohmios.
Sin hacer ninguna cuenta se adivina el valor haciendo la cuenta de la vieja.
Para e A) Me sale 6 ohmios y la solución que me da 2 ohmios. Lo que he hecho es hallar la resistencia en paralelo e igualarla a 3.
6 ohmios es correcto.
Como me lo ha explicado Albert es correcto. Pero gracias igualmente por tu tiempo
La solución de un problema es mejor cuanto más simple resulta de solucionar.
Para eso hallamos la conductancia de las resistencias y sumamos y restamos.
