Problema Elíptico en 2 Dimensiones

No sé exactamente como te lo habrán enseñado. Yo por lo encontrado se hace así. Seguramente mucho de lo que te diga ya lo tendrás en la teoría, pero por si acaso lo digo.

Aproximaremos las derivadas parciales por los valores de la función en puntos contiguos.

$$\begin{align}&\frac{\partial u(x,y)}{\partial x}= \frac{u(x+h,y)-u(x,y)}{h}\\ &\\ &\\ &\frac{\partial^2 u(x,y)}{\partial x^2}=\frac{u(x+h,y)-2u(x,y)-u(x-h,y)}{h^2}\\ &\\ &\end{align}$$

Se abrevia la escritura usando subíndices

Si

x = ih

y = jh

se escribe

$$u_{ij}=u(ih,jh)=u(x,y)$$

Con esta notación tendremos que la suma de las dos parciales segundas en el punto (x,y)=(ih,jh) es

$$\begin{align}&\frac{\partial^2 u(x,y)}{\partial x^2}+\frac{\partial^2 u(x,y)}{\partial y^2}= \\ &\\ &\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}+u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{h^2}=\\ &\\ &\frac{u_{i+1,j}+u_{i-1,j}+u_{i,j+1}+u_{i,j-1}-4u_{ij}}{h^2}=0\\ &\\ &Luego\\ &\\ &4u_{ij}=u_{i+1,j}+u_{i-1,j}+u_{i,j+1}+u_{i,j-1}\\ &\end{align}$$

Que se entiende perfectamente si lo interpretamos como el valor del punto medio es la cuarta parte de la suma de los puntos arriba, abajo, izquierda y derecha.

Voy a hacer un tramado con h=1 con lo que solo vamos a calcular el valor de la función en los puntos interiores (2,2) y (3,2) que serán u22 y u32

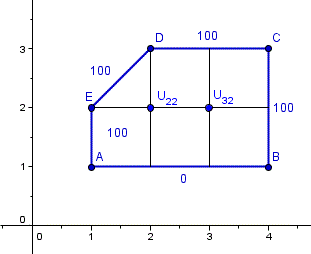
Las ecuaciones aplicadas a esos dos puntos son:

$$\begin{align}&4u_{22}= u32+100+100+0\\ &4u_{32}= 100+u_{22}+100+0\\ &\\ &\\ &\\ &u_{32}=4u_{22}-200\\ &\\ &4(4u_{22}-200) = u_{22}+200\\ &\\ &16u_{22}-800=u_{22}+200\\ &\\ &15u_{22}=1000\\ &\\ &u_{22}= \frac{1000}{15}= \frac{200}{3}= 66.666...\\ &\\ &u_{32}=4u_{22}-200=\frac{800}{3}-200=\frac{200}{3}= 66.666...\end{align}$$

Y eso es todo, espero que sea lo que pedías y lo hayas entendido.