a) La fórmula del volumen para una función girando en torno del eje X es:
$$V=\pi\int_{x_0}^{x_1}[f(x)]^2dx$$Los límites son líneas verticales de ecuación y=xo, y=x1 y la función del integrando es una función de x, o sea y=f(x)
Cuando el área está limitada entre dos funciones se calcula el volumen generado por la más externa y se le resta el volumen generado por la interior. Si las curvas se cruzan hay que dividir en trozos y hacer integrales en cada trozo.
En este caso de girar en torno a X no se resta ningún volumen ya que la curva interior es y=0 que no genera ningún volumen por ser el eje de giro.
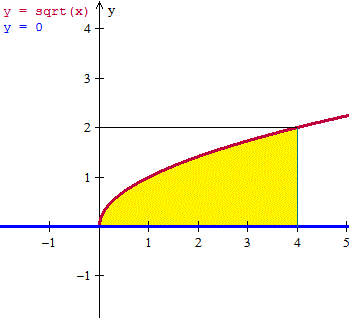
$$\begin{align}&V=\pi\int_0^4(\sqrt x)^2dx=\pi\int_0^4xdx=\\ &\\ &\pi \left. \frac{x^2}{2}\right|_0^4=\pi \frac{16}{2}=8\pi\end{align}$$b) Cuando gira respecto al eje Y la fórmula es
$$V=\pi\int_{y_0}^{y_1}g(y)dy$$La función hay que ponerla en la forma x=g(y). Si antes la teníamos como función de x
y=f(x) ahora será x=f^-1(y)
Y los límites son ahora líneas horizontales y=yo, y=y1
La función es y=sqrt(x) luego en función de y es x=y^2
Los límites de integración en y son 0 y 2
Y esta vez hay que tener en cuenta que hay un hueco, el volumen exterior lo genera la función x=4 y el interior la función x=y^2
El volumen será:
$$\begin{align}&V=\pi\int_0^24^2dy-\pi\int_0^2(y^2)^2dy=\\ &\\ &\\ &\pi\int_0^2(16-y^4)dy =\\ &\\ &\\ &\pi \left[16x-\frac{y^5}{5} \right]_0^2=\\ &\\ &\pi\left(32-\frac{32}{5} \right)=\frac{128}{5}\pi\end{align}$$Y eso es todo.


