Funciones de variable compleja
1.Dados los números complejos
$$\begin{align}&z_1=1+i \\ &z_2=-1-i\end{align}$$Hallar los números complejos
$$z_3$$
tales que los puntos
$$z_1,z_2,z_3$$
formen un triangulo equilátero
1 Respuesta
Este es un problema de geometría disfrazado de números complejos.
Con el dibujo se entenderá todo. Dibujaremos los números complejos que son equivalentes a los puntos (1,1) y (-1,-1). Luego el lado que determinan que es la bisectriz de los ejes y la mediatriz que es la otra bisectriz de los ejes.
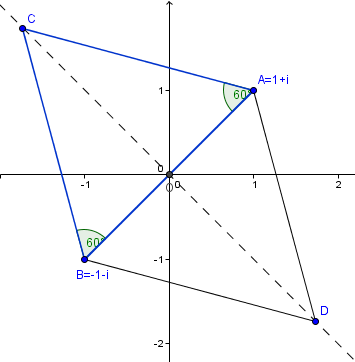
Sobre los puntos A y B habrá que dibujar ángulos de 60º. En el dibujo lo he hecho hacia el punto superior C pero lo mismo se hace hacia el punto D.
Y ahora hay que hacer unas pocas cuentas.
La distancia AC será igual a AB, la cual es
sqrt(2^2+2^2) = 2sqrt(2)
La distancia OC será
OC = AC·sen(60º) = 2sqrt(2)·sqrt(3)/2 = sqrt(2)sqrt(3)
Y las coordenadas (x,y) del punto C son iguales en módulo y su valor es
|x| = y = OC · cos(45º) = sqrt(2)·sqrt(3)·sqrt(2) / 2 = 2sqrt(3)/2 = sqrt(3)
Como C está en el segundo cuadrante son coordenadas son
C=(-sqrt(3), sqrt(3))
Que representan al número complejo
- sqrt(3) + i·sqrt(3)
Y el punto D es el simétrico respecto a O y es el número complejo
Sqrt(3) - i·sqrt(3)
Y eso es todo.
