Encontrar la medida de un ángulo
Espero me ayudes con ésto:
En el lado BC de un triángulo ABC se ubica el punto P de manera que AC+CP=PB.
Sea R el punto medio de AB.
Si la medida del ángulo RPB es de 43°, encuentra la medida del ángulo ACB.
Gracias.
1 Respuesta
No es una pregunta fácil y podría resolverla de forma muy distinta a como se supone que hay que resolverlo
Puedes decirme que es lo que estáis estudiando y de qué va el capítulo. Es muy distinto si es geometría con coordenadas que si es el tema de los teoremas del seno y coseno, si es geometría proyectiva, etc.
En el caso de que sea un ángulo único, que eso no lo he demostrado todavía, sería 86º que es el ángulo que se forma cuando AC = BC y el punto P se pone sobre C. Ya que se forma un triangulo isosceles donde RPB es la mitad del ángulo ABC.
Pero la demostración de que el ángulo es único no la tengo todavía y me vendría bien que me dijeras lo que estáis estudiando.
He aquí la figura
El centro de la circunferencia grande es F.. Se trata de demostrar que para todo punto C de ella entre A y C2, y tomando como P la intersección con la circunferencia pequeña del segmento BC se cumple AC+CP = PB. No es tan sencillo y ahora tengo que dejarlo.
ACB es un arco capaz, por eso mide siempre lo mismo para cualquier punto C y se ha construido para que sea 86º
También RPB es un arco capaz que se construyo de forma que midiera siempre 43º independientemente de P.
Para que se cumplieran esas cosas se tomaron estos puntos
B = (sen43º, -cos 43º)
R = (-sen43º, -cos 43º)
A = (-3sen43º, -cos43º)
Y de ahí se dedujo
C2 = (-sen43º, cos43º)
F = (-sen43º, cos43º - 2sen43º/cos4º)
Y supongo que ahora habría que aplicar geometría analítica para demostrarlo, pero ahora tengo que dejarlo.
Hola! Gracias.
Pues la materia en sí no es de geometría. Pero el maestro dijo que lo hiciéramos aplicando geometría euclidiana. Estaba pensando en trazar una paralela al segmento RP por el punto A, y prolongar el lado AC.
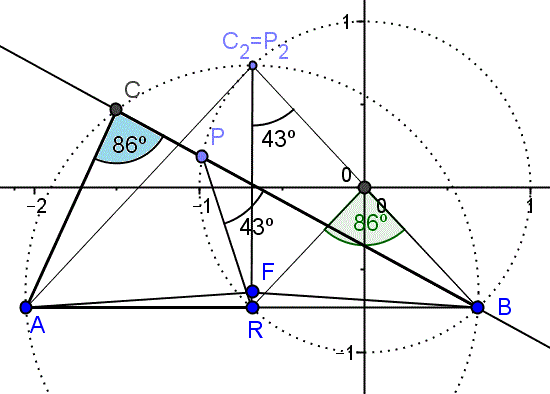
Consideremos el triángulo PBR, vamos a calcular el lado BP. Por el teorema de los senos
BP / senR = RB / senP
BP / senR = 2sen43º / sen 43º
BP = 2·senR
Nos hará falta ponerlo todo en función del ángulo B
B+R+43º = 180º
R = 137º-B
BP = 2sen(137º-B) = 2(sen137ºcosB - cos(137ºsenB) =
BP = 2sen43ºcosB + 2cos43ºsenB
Ahora consideramos el triángulo ABC y calculamos AC por el teorema de los senos
AC / senB = AB / senC
AC / senB = 4sen43º / sen86º = 4sen43º / 2sen43ºcos43º = 2/cos43º
AC = 2senB/cos43º
Ahora calcularemos BC, de nuevo por el teorema de los senos
BC / senA = AB / senC
BC / senA = 4sen43º / sen86º = 4sen43º / 2sen43ºcos43º = 2/cos43º
BC = 2senA/cos43
Como A+B+86º = 180º
A = 94º - B
BC = 2sen(94º-B)/cos43º =
2sen(180º-94º+B)/cos43º =
2sen(86º+B)/cos43º=
2(sen86ºcosB+cos86ºsenB)/cos43º=
2{2sen43ºcos43ºcosB + [cos^2(43º) - sen^2(43º)]senB} / cos43º
Debe cumplirse
BP = AC + CP = AC + BC - BP
2BP = AC + BC
Veamos
2BP = 4(sen43ºcosB + cos43ºsenB)
AC+BP = [2senB +2(sen94ºcosB-cos94ºsenB)]/cos43º
Pues he hecho cuentas aparte y no se llega a ninguna conclusión con esto del teorema de los senos.
Entonces dices la geometría esta de los puntos, vectores, ecuaciones de rectas, circunferencias, etc. Que se resuelven las cosas principalmente por ecuaciones.
Confírmamelo.
Pues es la de Euclides, semejanza de triangulo, segmentos, a lados iguales se oponen ángulos iguales.. etc.
No lo veo tan fácil, por geometría euclidiana se entiende la basada en los postulados de Euclides y es extensísima, también entra la geometría de tipo más algebraico que nada. Lo llevo pensando todo el rato, pero también tengo que responder otras preguntas, incluso algunas bastante complicadas que tengo acumuladas. No obstante ya sabes que si hay un ángulo único ese es 86º.
Si puedo lo intentaré.
