Grupos y subgrupos.. Álgebra Moderna?

Del teorema 3.1 de los apuntes se usa muchas veces la equivalencia de i y iii. Suele expresarse de esta forma.

Sea G un grupo y H un subconjunto de G. Entonces H es un subgrupo de G si y solo si se cumplen estas dos cosas:

i) H no es vacío

ii) Para todo a, b € H se cumple a·b^-1 € H

1) GL(n,K) es un grupo.

Es interna porque el producto de dos matrices nxn es otra matriz nxn

Es asociativa por serlo el producto de matrices.

Tiene elemento neutro porque la matriz identidad nxn es invertible, la inversa es ella misma

Cada matriz de GL(n, K) tiene su inversa en GL(n, K), porque si A es invertible entonces A^-1 también lo es.

2) SL(n,R) es un grupo

Las matrices nxn cuyo determinante es 1 son invertibles pues lo son todas aquellas cuyo determinante es distinto de cero.

Veamos que forman un subgrupo de GL(n, R) mediante la versión del teorema 3.1 que puse arriba

i) SL(n, R) no es vacío porque la matriz identidad tiene determinante 1

Ii) Sean Ay B matrices con determinante 1

Sabemos que el determinante del producto de dos matrices es el producto de los determinantes, lo aplicamos a B € SL(n, R) y B^-1

|B·B^-1| = |Id|=1

|B|·|B^-1| = 1

1·|B^-1| = 1

|B^-1| = 1

y finalmente

|AB^-1|=|A|·|B^-1| = 1·1 =1

luego AB^-1 € SL(n,R)

3) O(n) es grupo

Como en 2 usaremos el teorema para ver que un subgrupo de GL(n,R)

i) Tiene algún elemento puesto que la identidad por la identidad transpuesta da la identidad

ii) Sean Ay B matrices de O(n) tenemos que ver que

A·B^-1 € O(n)

Para ello debe suceder que el producto por su transpuesta sea la identidad. Usaré la prima para expresar la matriz transpuesta.

(A·B^-1)' · (AB^-1) = Id

Primero veamos que B^-1 también pertenece a O(n)

B' · B = Id

Multiplicamos a la derecha por B^-1

B' · B · B^-1 = B^-1

B' = B^-1

Multiplicamos a la izquierda por (B')^-1

(B')^-1 · B' = (B')^-1 · B^-1

Id = (B')^-1 · B^-1

Vaya, hay que demostrar que (B')^-1 = (B^-1)' para poder continuar

B·B^-1 = Id

(B·B^-1)' = Id

(B^-1)' · B' = Id

multiplicando a derecha por (B')^-1

(B^-1)' · B' · (B')^-1= (B')^-1

(B^-1)' ·= (B')^-1

Y volvemos a la línea anterior a la demostración y sustituimos

Id = (B^-1)' · B^-1

Luego B^-1 € O(n)

Y ahora veamos que

(A·B^-1)' · (AB^-1) = Id

usaremos que (CD)' = D' · C'

(B^-1)' · A' · A · B^-1 =

Como A € O(n)

(B^-1)^t · Id · B^-1 =

(B^-1)^t · B^-1=

Como B^-1 € O(n) tal como demostramos

= Id

Luego O(n) es un subgrupo de GL(n, R)

4) SO(n) son los elementos de O(n) con determinante 1.

De modo análogo a como se hizo en 2 se comprueba que son un subgrupo de O(n). No tiene nada especial la comprobación.

5) SL(n, Q) se comprueba que es grupo porque es subgrupo de SL(n, R). Las matrices con coeficientes racionales tienen la identidad, sus inversas son racionales y su producto también. Con esos elementos podemos emplear el teorema de caracterización de los subgrupos y demostrar que lo son.

6) SL(n, Z) es un grupo, lo podemos comprobar como subgrupo de SL(n, Q).

Lo que tiene algo especial es demostrar que la operación es interna y tiene inverso en el propio SL(n.Z)

El producto de matrices enteras es entero, eso no ofrece problema. La inversa de una matriz entera no tiene porque ser entera, pero si el determinante es 1 sí lo es, porque los elementos de la inversa se obtienen como adjuntos (operaciones suma, resta y producto sobre los elementos de la matriz que dan resultado entero) divididos entre el determinante que es 1, luego los elementos de la inversa son enteros.

Este es el diagrama reticular de los subgrupos, en los que están conectados el que está situado abajo es subgrupo del superior.

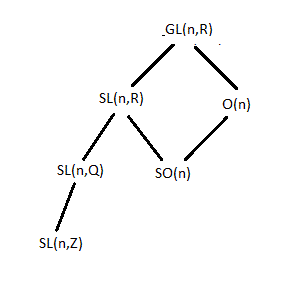
Y eso es todo.