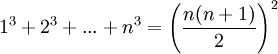Si se supone que el resultado es un polinomio de grado 4, entonces será el único polinomio que pase por 5 puntos correspondientes a la suma de cubos
Así será un polinomio que pase por los puntos
(1,1)
(2, 1+8) = (2,9)
(3, 9+27) = (3,36)
(4, 36+64) = (4, 100)
(5, 100+125) = (5, 225)
Y el cáculo del polinomio se hace por la fórmula de Lagrange o de Newton. Ambas las tengo completamente olvidadas. Mejor el método de Newton.
Puede que la tabla quede desastrosa si se comen los espaciós en blanco que voy a poner o les dan una longitud distinta a la que hay mientras escribo, puede pasar
Las diferencias divididas son:
f(xi) f[xi,x(i+1)] f[xi,..,..] f[xi,,,] f[xi,,,,]
xo 1 1 8 19/2 3 1/4
x1 2 9 27 37/2 4
x2 3 36 64 61/2
x3 4 100 125
x4 5 225
Y de acuerdo con la teoría sobre diferencias divididas y el polinomio de inrterpolación de Newton tenemos:
p4(x) = f(xo) + f[xo,x1](x-xo) + f[xo,x1,x2](x-xo)(x-x1) + f[xo,x1,x2,x3](x-xo)(x-x1)(x-x2) + f[xo,x1,x2,x3,x4] (x-xo)(x-x1)(x-x2)(x-x3) =
1 + 8(x-1) + (19/2)(x-1)(x-2) + 3(x-1)(x-2)(x-3) + (1/4)(x-1)(x-2)(x-3)(x-4) = ...
las cuentas se dejan como ejercicio
... = (x^4+2x^3+x^2) / 4
Comprobamos para algún valor
p4(1) = 4/4=1
p4(2) = (16+16+4)/4 = 36/4 = 9
p4(6) = (1296 + 432 + 36) / 4 = 441
Teníamos que la suma hasta 5 era 225 + 6^3 = 225+216 = 441
Luego ha acertado para un número de fuera de la lista con que se confeccionó, estará bien.
1^3+2^3+ ...+ n^3 = (n^4 + 2n^3 + n^2) / 4
Se puede simplificar para hacer más fácil las cuentas
$$\begin{align}&\frac{n^4+2n^3+n^2}{4} = \frac{n^2(n^2+2n+1)}{4}=\\ &\\ &\frac{n^2(n+1)^2}{4} = \left(\frac{n(n+1)}{2}\right)^2\end{align}$$Y solo con una multiplicación, una división fácil y un cuadadro haces los cáculos
Si buscas la fórmula para estar seguro encontrarás
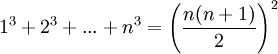
en
http://es.wikipedia.org/wiki/Cubo_%28aritm%C3%A9tica%29
Es posible que por un fallo de la página no puedas pinchar y tengas que copiar y pegar la dirección en la barra del navegador para poder ver al artículo, es un fallo de esta página.
Y eso es todo, espero que te sirva y lo hayas entendido. Lo he hecho rápido suponiendo que estás dando esta materia de Análisis Numérico, porque el problema es claramente de esa materia.