Probabilidad de acierto al elegir opciones ocultas.
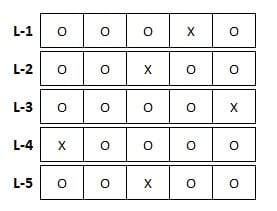
Según la imagen anterior. Tenemos 5 líneas horizontales L-1, L-2, L-3, L-4, L-5 estas tienen 5 casillas cada una con 1 (X) y 4 (O). Suponiendo que cada casilla de estas están ocultas y que debemos descubrir solo una de cada línea. Ósea descubriremos 5 casillas, una de cada línea.
Sabiendo esto que probabilidad hay de:
- Que las 5 casillas descubiertas sean X (XXXXX)
- Que las 4 casillas primeras sean x y la 5ta O (XXXXO)
- Que la primera casilla descubierta sea una O y las 4 siguiente X (OXXXX)
- Que las 3 primeras X y las 2 siguientes O (XXXOO)
- Que las 3 primeras sean O y las 2 siguientes X (OOOXX)
mas importante que me den esta respuesta es que me expliquen como hacerlo yo mismo.
Respuesta de Lucas m
1

