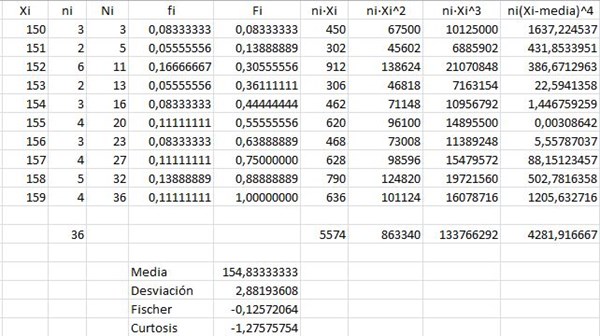
Casi finalizamos ahora; medidas de curtosis
Ahora vamos a desarrollar un estudio de estadística descriptiva, para datos AGRUPADOS.
Bueno ahora, nos proporcionan los reportes mensuales de los últimos tres años…
2007 2008 2009
151 156 154 152 157 155 153 159 158
152 150 152 157 158 159 158 157 155
152 151 155 156 152 155 159 154 153
152 154 150 159 158 150 156 158 157
Ahora has un estudio descriptivo…pero ahora para datos AGRUPADOS…
Entonces que debemos de hacer… MEDIDAS DE CURTOSIS
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1