Anónimo
Determina la ecuación de regresión.
Podrían ayudarme con este ejercicio, gracias.
x (cm) y (kg)
152 50
155 61.5
152 54.5
155 57.5
157 63.5
152 59
157 61
165 72
162 66
178 72
183 84
178 82
Los datos de la tabla anterior representan la estatura y el peso de un grupo de 12 personas. La estatura en centímetros se representa en (x) y el peso en kilogramos se representa en (y). Revisa los datos y responde las preguntas.
1. Determina la ecuación de regresión.
2. Ramiro mide 169 cm, ¿cuál sería su peso?
3. Carlos mide 167 cm, ¿cuál sería su peso?
4. Ramiro pesa 74 kg mientras que Carlos pesa 98 kg, ¿qué puedes decir sobre los valores (pesos) reales en comparación con los que se obtienen en la recta de regresión?
2 Respuestas
¿Tienes alguna restricción para resolver los ejercicios? Te lo pregunto porque resolverlo a mano es muy laborioso (no es difícil, pero lleva muchos cálculos, tiempos y probabilidad de error). Lo que te recomiendo es que metas esta tabla en una planilla excel, luego
1. Inserta un gráfico de dispersión con los datos ingresados
2. Pide la curva de regresión (marcando la opción que te muestre la ecuación en el gráfico).
3. Listo
Si hiciste lo anterior, te dice que la curva de regresión lineal es y=0,8676x - 75,443
En base a esto vamos a contestar las preguntas:
1. Listo
2. Reemplazando en la ecuación, y = 0,8676*169-75,443= 71,18. Ramiro pesaría 71 Kg
3. Idem y = 0,8676*167-75,443= 69,45. Carlos pesaría 69Kg
4. En el caso de Ramiro, está dentro de los valores esperables de la ecuación, Mientras que Carlos queda obviamente muy por fuera de la misma y la recta no lo representaría.
·
1)
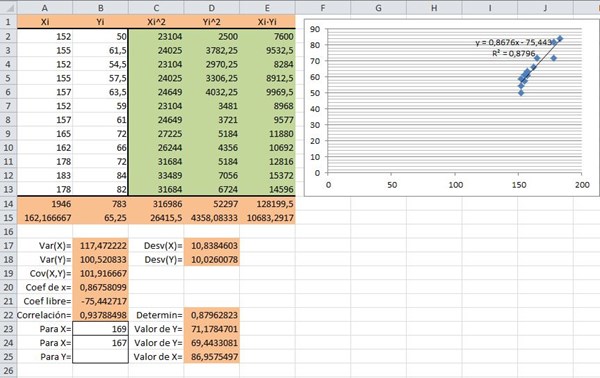
Como me mandan algunos ejercicios de estos y se necesita hacer muchas cuentas tengo hecha una tabla de Excel que las hace y solo tengo que meter los datos.
Te dejo las fórmulas por si no las conoces
$$\begin{align}&recta:\quad y = \overline y+\frac{Cov(X,Y)}{\sigma^2_X}(x-\overline x)\\ & \\ & \overline x=\frac{\sum_{i=1}^n X_i}{n}\\ & \\ & \overline y=\frac{\sum_{i=1}^n Y_i}{n}\\ & \\ & \sigma^2_X=\frac{\sum_{i=1}^n X_i^2}{n}- (\overline x)^2\\ & \\ & Cov(X,Y) =\frac{\sum_{i=1}^n X_iY_i}{n}- \overline x·\overline y\end{align}$$y si necesitas alguna explicación pídemela.
Entonces la hoja lo hace todo pero vamos a aprovechar solo la parte de los cálculos más pesados
LLegamos a que
media de Xi = 162.166666
media de Yi = 65.25
Varianza de X = 117.472222
Covarianza de X e Y = 101.916666
Con esto datos vamos a la fórmula de la recta de regresión
$$\begin{align}&y = \overline y+\frac{Cov(X,Y)}{\sigma^2_X}(x-\overline x)\\ & \\ & y = 65.25+\frac{101.916666}{117.472222}(x-162.166666)\\ & \\ & y = 65.25 + 0.8675809895(x-162.166666)\\ & \\ & y =65.25 + 0.8675809895x-140.6927166\\ & \\ & y= 0.8675809895x - 75.44271655\end{align}$$·
2)
Y una vez tenemos la recta lo demás ya es facil
Ramiro
y = 0.8675809895 · 169 - 75.44271655 = 71.17847068 kg
·
3)
Carlos
y = 0.8675809895 · 167 - 75.44271655 = 69.4433087 kg
·
4) El peso de Ramiro esta relativamente cerca de lo que dice la recta. El de Carlos está muy alejado, tanto que te pido revises el enunciado, ¿tal vez ponga 68 en vez de 98?