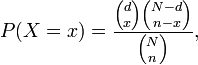Como se hace este problema , creo que es de distribución de probabilidad?
2. Los procedimientos de muestreo para aceptar lotes en una empresa manufacturera electrónica requiere el muestreo de n artículos de un lote de N artículos, y aceptar el lote si X ≤ c, donde X es el número de artículos defectuosos en la muestra. Para un lote de 20 cubiertas de impresoras, se debe mostrar 5. Calcular de aceptar el lote si c = 1, y si el número real de cubiertas defectuosas en el lote es:
a) X = 0, 1, 2, 3, 4
b) Responder la anterior preguntase c = 2.
1 Respuesta
·
La distribución que se usa en estos casos es la hpergeométrica:
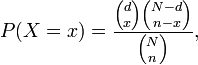
donde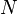 
es el tamaño de población, 
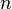es el tamaño de la muestra extraída, 
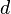es el número de elementos en la población original que pertenecen a la categoría deseada y 
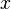es el número de elementos en la muestra que pertenecen a dicha categoría.
a) No ha estado bien llamar X a las defectuosas, ese número se corresponde con el que hemos llamado d. Así que corrijo el enunciado y digo, hallar la probabilidad de aceptar el lote si el número real de defectuosas es d=0, 1,2,3,4. Se aceptará el lote si el número de defectuosas es 1 ó 0, luego para d=0 y d=1 no es necesario hacer ninguna cuenta, se aceptará siempre.
$$\begin{align}&Si \;d=2\\&\\&P(0)=\frac{\binom 2 0\binom{20-2}{5-0} }{\binom{20}{5}}=\frac{1·\frac{18!}{5!·13!}}{\frac{20!}{5!·15!}}\\&\\&=\frac{15·14}{20·19}=\frac{210}{380}=\frac{21}{38}\\&\\&P(1) =\frac{\binom 2 1\binom{20-2}{5-1} }{\binom{20}{5}}=\frac{2·\frac{18!}{4!·14!}}{\frac{20!}{5!·15!}}=\\&\\&\frac{2·5·15}{20·19}=\frac{150}{380}=\frac{15}{38}\\&\\&P(0)+P(1) =\frac{21+15}{38}=\frac{36}{38}=0.9473684211\\&\\&--------------------\\&\\&Si \;d=3\\&\\&P(0)=\frac{\binom 3 0\binom{20-3}{5-0} }{\binom{20}{5}}=\frac{1·\frac{17!}{5!·12!}}{\frac{20!}{5!·15!}}\\&\\&=\frac{15·14·13}{20·19·18}=\frac{2730}{6840}=\frac{91}{228}\\&\\&P(1) =\frac{\binom 3 1\binom{20-3}{5-1} }{\binom{20}{5}}=\frac{3·\frac{17!}{4!·13!}}{\frac{20!}{5!·15!}}=\\&\\&\frac{3·5·15·14}{20·19·18}=\frac{3150}{6840}=\frac{35}{76}\\&\\&P(0)+P(1) =\frac{91+105}{228}=0.8596491228\\&\\&------------------\\&\\&Si \;d=4\\&\\&P(0)=\frac{\binom 4 0\binom{20-4}{5-0} }{\binom{20}{5}}=\frac{1·\frac{16!}{5!·11!}}{\frac{20!}{5!·15!}}\\&\\&=\frac{15·14·13·12}{20·19·18·17}=\frac{32760}{116280}=\frac{91}{323}\\&\\&P(1) =\frac{\binom 4 1\binom{20-4}{5-1} }{\binom{20}{5}}=\frac{4·\frac{16!}{4!·12!}}{\frac{20!}{5!·15!}}=\\&\\&\frac{4·5·15·14·13}{20·19·18·17}=\frac{54600}{116280}=\frac{455}{969}\\&\\&P(0)+P(1) =\frac{273+455}{969}=0.7512899897\end{align}$$·
b)
Como puedes ver el problema es muy pesado de cuentas pero no es muy difícil, te lo dejo. No tienes que volver a hacerlas todas porque las hechas te sirven.
En d=2 la probabilidad de aceptación será 1 ahora
En d=3 a la probabilidad que hay deberás sumarle la P(2) que calcules para d=3
En d=4 a la probabilidad que hay deberás sumarle la P(2) que calcules para d=4
·
Y eso es todo.
