¿Qué puedo hacer en este Problema de Geometría Analítica?
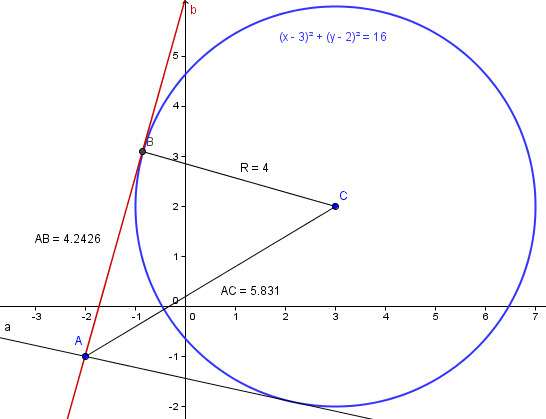
Desde el punto a (-2,-1) se traza una tangente a la circunferencia
$$\begin{align}&x^2+y^2-6x-4y-3=0\end{align}$$si B es el punto de contacto, hallar la longitud del segmento AB. Lo mas simple para no quitarle mucho tiempo al experto en responder gracias por su ayuda
2 respuestas
·
Debemos hallar el centro y radio de la circunferencia. Y despues usaremos el teorema de Pitagoras, ya que la tangente y el radio forman un ángulo de 90º, con lo cual se forma un triangulo rectángulo cuyos vértices son el punto, el centro y el punto de tangencia. La hipotenusa sera la distancia del punto al centro y los catetos el radio y la distancia del punto al punto de tangencia.
Dada la ecuación de una circunferencia si la pones en la forma
(x+h)^2 + (y-k)^2 = R^2
Tendrás que (h, k) es el centro y R el radio.
El método para obtrener esa ecuación canónica se llama completar cuadrados, consiste en hacer sustituciones de este tipo
a^2 + 2ab = (a+b)^2 - b^2
que puedes comprobar son válidas ya que
(a+b)^2 - b^2 = a^2 + 2ab + b^2 - b^2 = a^2 + 2ab
Entonces tomaremos (x^2 -6x) y (y^2-4y) y haremos esas sustituciones.
$$\begin{align}&x^2+y^2-6x-4y-3=0\\&\\&(x^2-6x)+ (y^2-4y)-3=0\\&\\&[(x-3)^2-9] + [(y-2)^2-4]-3=0\\&\\&(x-3)^2+(y-2)^2-9-4-3=0\\&\\&(x-3)^2+(y-2)^2=16=4^2\\&\\&\text{Luego el centro es }C(3,2) \;y\; R=4\\&\\&\text{Siendo A(-2,-1) y B en punto de tangencia}\\&\\&\text{El teorema de Pitagorás será}\\&\\&R^2+ \overline {AB}^2= \overline{AC}^2\\&\\&4^2+\overline {AB}^2=(3-(-2))^2+(2-(-1))^2\\&\\&16+\overline {AB}^2=25+9=34\\&\\&\overline{AB}^2=34-16=18\\&\\&\overline{AB}=\sqrt {18}=3 \sqrt 2\approx4.24264068\end{align}$$Y esta es la gráfica.
·
Lo primero es completar cuadrados para ver cual es el centro de la circunferencia (y el radio).
$$\begin{align}&x^2+y^2-6x-4y-3=0\\&Reacomodo,\ sumo\ y\ resto\ 4\ y\ 9\\&x^2-6x+9+y^2-4y+4-3-9-4=0\\&(x^2-6x+9)+(y^2-4y+4)-16=0\\&(x-3)^2+(y-2)^2=4^2\\&\\&\end{align}$$O sea, que la circunferencia tiene centro en el punto (3,2) y tiene radio 4.
Primero, nos aseguramos que el punto (-2,-1) no pertenece a la circunferencia (si es así, no hay nada que hacer).
(-2-3)^2 + (-1-2)^2 = 25+9 = 34 distinto de 16 por lo tanto, está bien y no pertenece
La longitud del segmento AB será
$$\begin{align}&\overline{AB}=\sqrt{distancia(A,C)^2+R^2}\\&distancia(A,C)= distancia[(-2,-1),(3,2)]=\sqrt{(-2-3)^2+(-1-2)^2}=\sqrt{34}\approx5,83\\&\overline{AB}=\sqrt{34+16}=\sqrt{50}\approx7,071\\&\\&\end{align}$$Te dejo un link con la teoría para deducir la longitud del segmento AB
https://www.edistribucion.es/anayaeducacion/8440049/datos/09/CDa_t09_07_3eso_mec.pdf
Te dejo una corrección a mi ejercicio y es que la distancia entre A y B forman la hipótenusa del triángulo rectángulo, por lo que en realidad el segmento AB mide
$$\begin{align}&\overline{AB}=\sqrt{distancia(AC)^2-R^2}\\&\overline{AB}=\sqrt{(\sqrt{50})^2-16}\\&\overline{AB}=\sqrt{(\sqrt{34})^2-16} = \sqrt{18}\approx4,24\\&\end{align}$$