Valores K para que los dos sistemas sean equivalentes? Álgebra analitica
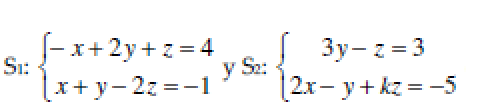
valores K para que los dos sistemas sean equivalentes? resuelto desde el álgebra analítica
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
