Duda con problema de geometria analitica.
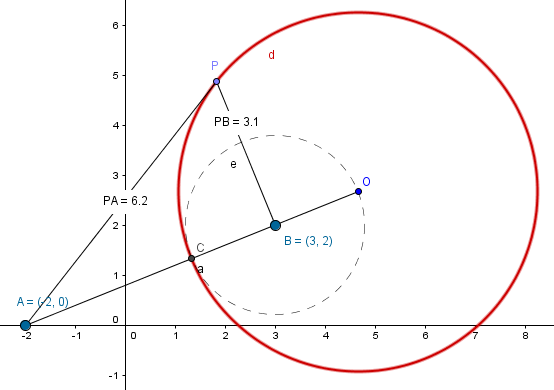
Hallar la ecuación del lugar geométrico de los puntos P(x, y) cuya distancia a A(-2,0) se a el doble de la de B(3,2) 3x2+3y2-28x-16y+48=0
2 Respuestas
Respuesta de Lucas m
1
La distancia entre dos puntos es el módulo del vector:
$$\begin{align}&\vec{AP}=P-A=(x,y)-(-2,0)=(x+2,y)\\&|\vec{AP}|=\sqrt{(x+2)^2+y^2}\\&\\&\vec{BP}=P-B=(x,y)-(3,2)=(x-3,y-2)\\&\\&|\vec{BP}|= \sqrt{(x-3)^2+(y-2)^2}\\&\\&dist(A,P)=2dist(B,P)\\& |\vec{AP}|=2|\vec{BP}|\\&\\&\sqrt{(x+2)^2+y^2}=2 \sqrt{(x-3)^2+(y-2)^2}\\&Elevando \ al \ cuadrado:\\&\\&(x+2)^2+y^2=4 \Bigg[ (x-3)^2+(y-2)^2 \Bigg]\\&\\&x^2+4x+4+y^2=4(x^2-6x+9+y^2-4y+4)\\&\\&0=3x^2+3y^2-28x-16y+48\end{align}$$Saludos
:
:
Respuesta de Valero Angel Serrano Mercadal
1
¡Gracias!
Calculamos las distancias de un punto genérico P(x, y) a los dos puntos y aplicamos la ecuación
$$\begin{align}&d(A,P)= \sqrt{(x+2)^2+y^2}\\&\\&d(B,P) = \sqrt{(x-3)^2+(y-2)^2}\\&\\&\text{como la primera es el doble que la segunda}\\&\\& \sqrt{(x+2)^2+y^2}= 2 \sqrt{(x-3)^2+(y-2)^2}\\&\\&\text{elevamos al cuadrado}\\&\\&(x+2)^2+y^2=4((x-3)^2+(y-2)^2)\\&\\&x^2+4+4x + y^2 = 4(x^2+9-6x+y^2+4-4y)\\&\\&x^2+4+4x + y^2 = 4x^2+36-24x+4y^2+16-16y\\&\\&\text{lo pasamos todo a la derecha}\\&\\&3x^2+3y^2-28x-16y+48=0\\&\end{align}$$Lo cual es la ecuación de una circunferencia, es facil calcular el centro
(28/6, 16/6)
El radio cuesta un poquito más. Pero como esto ya es un extra a la pregunta usaré Geogebra para todo.
Es curioso esto. Dividimos el segmento AB en tres partes y añadimos una de ellas a B a la derecha en la recta y obtenemos el centro. El radio es 2/3 de la distancia AB.
:
: