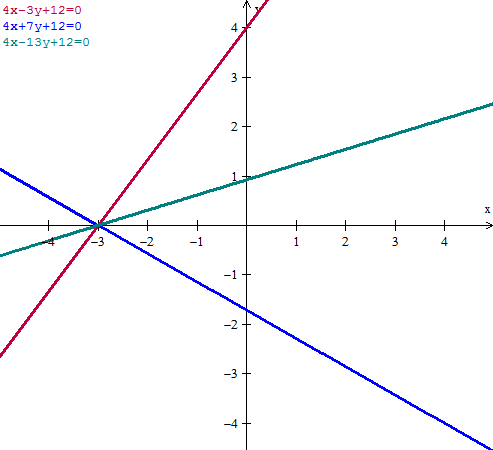Algunas dudas con un ejercicio de geometría analítica
Hallar la ecuación del lugar geométrico de un punto que se mueve de tal manera que la distancia de la recta 4x-3y+12=0 es siempre igual al doble de su distancia al eje por
4x+7y+12=0
Respuesta de Valero Angel Serrano Mercadal
1