Como solucionar Derivada de funciones trascendentes
Me podrían ayudar con estos ejercicios.
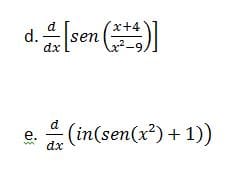
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Johan!
$$\begin{align}&d) \quad \frac d{dx}\left[sen\left(\frac{x+4}{x^2-9} \right) \right]=\\&\\&\cos \left(\frac{x+4}{x^2-9} \right) ·\frac{1·(x^2-9)-(x+4)·2x}{(x^2-9)^2}=\\&\\&\frac{x^2-9-2x^2-8x}{(x^2-9)^2}·\cos \left(\frac{x+4}{x^2-9} \right)=\\&\\&\frac{-x^2-8x-9}{(x^2-9)^2}·\cos \left(\frac{x+4}{x^2-9} \right)\\&\\&\\&\\&e) \frac{d}{dx}\left(ln(sen(x^2)+1\right)=\\&\\&\frac 1{sen(x^2)+1}·\cos(x^2)·2x =\\&\\&\frac{2x·\cos(x^2)}{1+sen(x^2)}\end{align}$$:
:
