Como desarrollar : Máximos, mínimos y gráfica de una función

·

·

¡Hola Julio!

Ahora no tengo tiempo, solo calcularé los máximos, mínimos y la gráfica será dentro de unas horas.

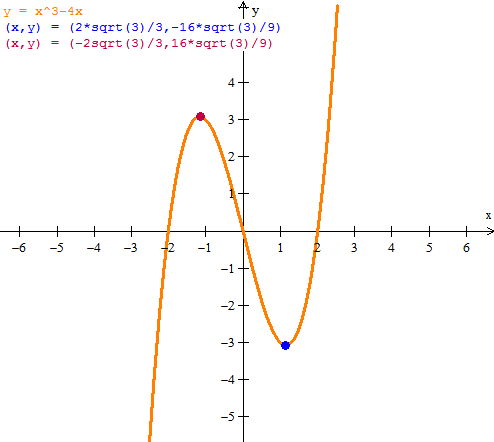
$$\begin{align}&f(x)=x^3-4x\\&\\&\text{derivamos e igualamos a 0}\\&\\&f'(x) = 3x^2-4=0\\&\\&3x^2=4\\&\\&x^2=\frac{4}{3}\\&\\&x=\pm \sqrt{\frac 43}=\pm \frac{2}{\sqrt 3}=\pm \frac {2 \sqrt 3}{3}\\&\\&\text{Calculamos la derivada segunda}\\&\\&f''(x)=6x\\&\\&f''\left( \frac {2 \sqrt 3}{3}  \right)= 6·\left( \frac {2 \sqrt 3}{3}  \right)>0\implies mínimo\\&\\&f''\left( \frac {2 \sqrt 3}{3}  \right)= 6·\left(- \frac {2 \sqrt 3}{3}  \right)\le0\implies máximo\\&\\&\\&\text{Calculemos el valor de la función en ellos}\\&\\&f\left( \frac {2 \sqrt 3}{3}  \right)=\left( \frac {2 \sqrt 3}{3}  \right)^3-4\left( \frac {2 \sqrt 3}{3}  \right)=\\&\\&\frac{8·3 \sqrt 3}{27}-\frac {8 \sqrt 3}{3}=\frac{8 \sqrt 3}{9}-\frac {8 \sqrt 3}{3}=\\&\\&\frac{8 \sqrt 3-24 \sqrt 3}{9}=-\frac{16 \sqrt 3}{9}\\&\\&\\&f\left( -\frac {2 \sqrt 3}{3}  \right)=\left( -\frac {2 \sqrt 3}{3}  \right)^3-4\left( -\frac {2 \sqrt 3}{3}  \right)=\\&\\&-\frac{8·3 \sqrt 3}{27}+\frac {8 \sqrt 3}{3}=-\frac{8 \sqrt 3}{9}+\frac {8 \sqrt 3}{3}=\\&\\&\frac{-8 \sqrt 3+24 \sqrt 3}{9}=\frac{16 \sqrt 3}{9}\\&\\&\text{Luego el mínimo relativo es el punto}\\&\left( \frac {2 \sqrt 3}{3},  -\frac{16 \sqrt 3}{9}\right)\\&\\&\text{Y el máximo relativo es}\\&\\&\left(- \frac {2 \sqrt 3}{3},  \frac{16 \sqrt 3}{9}\right)\\&\\&\\&\end{align}$$

Y eso es todo de momento.

Saludos.

·

·