Leyes de Movimiento: Resolver el siguiente problema...
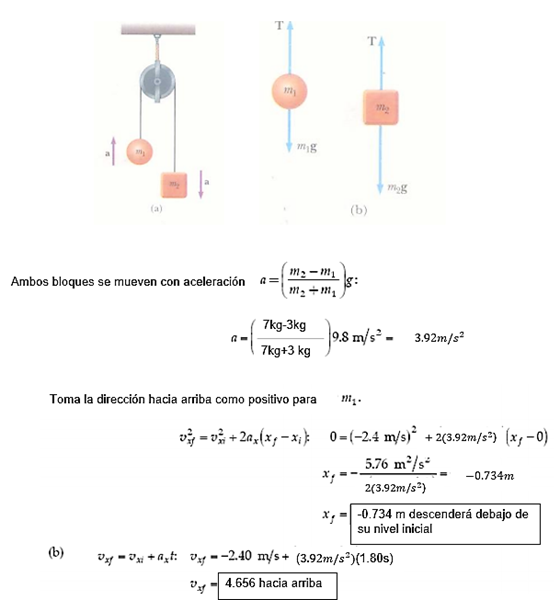
En la máquina de Atwood que se muestra en la figura,𝑚1 = 3.00 kg y𝑚2 = 7.00 kg. La polea tiene masa despreciable y gira sin fricción. La cuerda es muy liviana e inextensible, y es larga a ambos costados. El objeto más ligero se libera con un empujón rápido que lo pone en movimiento a 2.40 m/s hacia abajo. ¿Qué distancia descenderá𝑚1 por debajo del nivel donde fue liberado?
2 respuestas
Un placer ayudarte!
No olvides valorar las respuestas hermano.
Saludos!
El sistema como lo dibujas tendera naturalmente a desplazarse elevandose la m1 y descendiendo la m2. El movimiento de ambas masas vinculadas seras tipo uniformemente + acelerado con una aceleracion = (m2 - m1 / m2 + m1) g =0.40 g = 3.90 m/seg^2 (con g=9.80 m/seg^2,).
Se te sitúas del lado de la m1... la misma ascenderá con esa aceleración. Pero si la impulsas hacia abajo con vo = -2.40 m/seg. en principio la aceleración tenderá a frenarla...
Te piden cuanto descenderá ( frenándose) hasta detenerse:
Vfinal = 0 = -2.40 + 3.90 t .......................t = 2.40 / 3.90 = 0.615 seg.
Luego en la ecuacion del espacio tenes : y( 0.615 ) = Vo t + 1/2 3.90 t^2 =
(-2.40 x 0.615) + 1/2 x3.90 x 0.615^2 = - 1.476 + 0.737 = - 0.7385 m hacia abajo hasta detenerse.