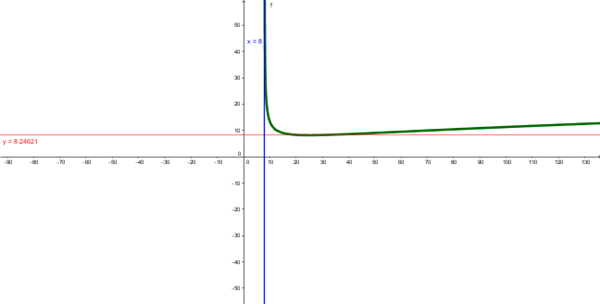
Para la función dada determine el respectivo dominio y rango

Buenas tardes amigos de todo expertos espero su ayuda con estos ejercicios
Respuesta de Valero Angel Serrano Mercadal
2
1 respuesta más de otro experto
Respuesta de Lucas m
2