Determinela rapidez del medicamento mientras sale de la punta de la aguja?
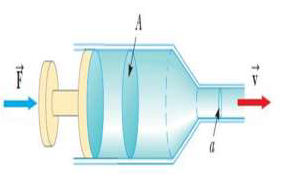
Una jeringa hipodérmica contiene un medicamento que tiene la densidad del agua El barril de la jeringa tiene un área de sección transversal A =2.50×10^-5 m² y la aguja tiene un área de sección transversal a =1.00 ×10^-8 m² En ausencia de una fuerza sobre el embolo, la presión en todas partes es 1 atm. Una fuerza𝑭⃗ de 2.00 N de magnitud actúa sobre el embolo, lo que hace que la medicina salpique horizontalmente desde la aguja. Determine la rapidez del medicamento mientras sale de la punta de la aguja.
1 Respuesta
Tienes que escribir dos ecuaciones: la ecuación de continuidad y el teorema de Bernouill.
El flujo ha de ser el mismo en la jeringa (punto 1) y en el extremo de la aguja (punto 2):
Densidad · S1 · v1 = densidad · S2 · v2
Como la densidad es la misma,
S1 · v1 = S2 · v2
2,5 · 10^(-5) · v1 = 10^-8 · v2
De aquí
v1 = 4 · 10^(-4) · v2
Ecuación de Bernouilli, teniendo en cuenta que la presión manométrica en el punto 1 vale
p1 = F / S = 2 / [2,5 · 10^(-5)] = 8 · 10^4 Pa
En el punto 2 la presión manométrica es 0.
La altura es la misma para los dos puntos, así que
p1 + v1^2 · d / 2 = p2 + v2^2 · d / 2
Sustituimos v1 en función de v2 de la ecuación de continuidad, y siendo d = 1000 kg / m^3
8 · 10^4 + [4 · 10^(-4) · v2]^2 · 1000 / 2 = 0 + v2^2 · 1000 / 2
8 · 10^4 + 8 · 10^(-5) v2^2 = 500 · v2^2
8 · 10^4 = 500 · v2^2 (despreciando el segundo término del primer miembro por ser mucho más pequeño que el segundo miembro).
v2 = 12,65 m/s
