A un tinaco de 4.5 m de alto se le hace un pequeño agujero debido al tiempo y la corrosión,este agujero se encuentra la corrosió
Corrosión, este agujero se encuentra justo en la base del tinaco. Deduce la fórmula para calcular la velocidad con que saldrá el chorro de agua por el agujero y calcula.
Desarrollo:
Partiendo de la ecuación de Bernoulli, toma en cuenta las consideraciones indicadas, realiza las sustituciones en la ecuación y escribe la expresión que resulta:
http://148.247.220.223/pluginfile.php/9217/mod_assign/intro/form.PNG
La velocidad en el punto más alto es insignificante comparada con la velocidad del chorro,
es decir: pv![]() / 2 = 0, entonces la expresión queda:
/ 2 = 0, entonces la expresión queda:
La presión en ambos puntos es aproximadamente la misma, es decir: P1=P2 o P1-P2 = 0, entonces la expresión resultante es:
De la expresión anterior considera que la altura en el punto más bajo es cero por lo que ρgh2 = 0, entonces la expresión simplificada queda como:
Despejando la velocidad de esta última expresión, la velocidad la podemos calcular con la fórmula:
a) v2=(2gh1)2
b) v2=![]()
c) v2=2gh1
Sustituye el valor de la altura del tinaco y calcula la velocidad con la que el agua sale por el agujero:
v=


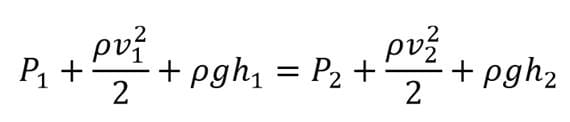
Hola estoy atorada para la resolución de este problema alguien me podría orientar saludos - Fabiola Victoria Pichardo Sanchez