Determine el tiempo que dura el proyectil en el aire. (en segundos)
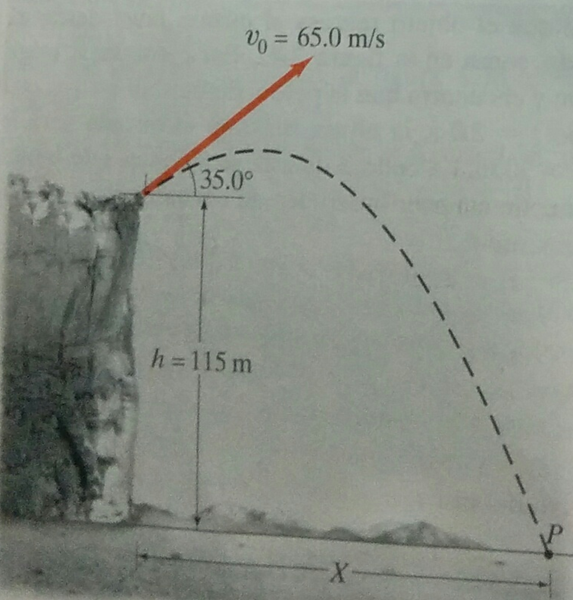
Se dispara un proyectil desde el borde de un acantilado que está a 115 m por encima del nivel del suelo, con una rapidez inicial de 65 m/s a un ángulo de 35° sobre la horizontal. A) Determine el tiempo que dura el proyectil en el aire. (En segundos)
b) Determine la distancia horizontal (x) recorrida. (En metros)
En el instante justo antes de que el proyectil toque el suelo, encuentre: c) La componente horizontal de su velocidad. (en m/s)
En el instante justo antes de que el proyectil toque el suelo, encuentre: d) La componente vertical de su velocidad. (en m/s)
e) Determine la altura máxima alcanzada por el proyectil. (En metros)
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
Respuesta de albert buscapolos Ing°
