Densidad de masa lineal y la cuerda
En la figura 27a, la cuerda #1 tiene una densidad de masa lineal de 3.31 g/m, y la cuerda # 2 de 4.87 g/m. Está bajo tensión debido al bloque colgante de masa M=511 g.(a) Calcule la velocidad de onda en cada cuerd. (b) El bloque se divide ahora en dos bloques (siendo
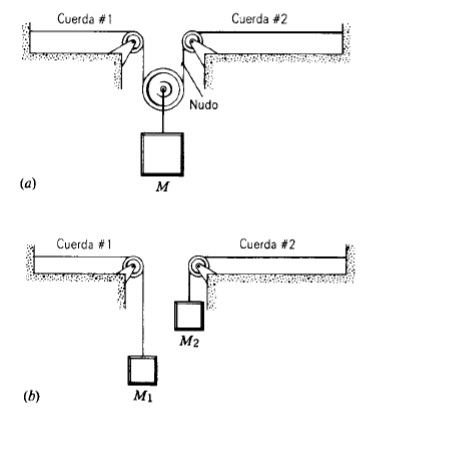
+M2 =M) y el aparato se modifica como se muestra en la 27b. Halle M1 y M, de modo las velocidades de onda de las dos cuerdas sean iguales.
1 Respuesta
a) La velocidad de una perturbación viajando por una cuerda tensa, estudiada ya por Galileo, depende de las variables P= tracción aplicada sobre el extremo libre y mu= densidad lineal de la misma.
La fórmula es simple... Velocidad de la perturbación = V( P/mu)
Siendo M= 0.511 Kg. masa y g = 9.80 m/s^2 .................la tension sobre cada una de las cuerdas 1 y 2 será la misma = 0.511 x 9.80 / 2 = 2.5 Newtons.
La velocidad de propagacion de una onda sobre cada cuerda seria:
Cuerda 1 = V( 2.5 / 0.00331) = 27.5 m/seg.
Cuerda 2 = V( 2.5 / 0.00487) =22.65 m/seg.
b) Ahora las cuerdas se separan. Cuerda 1 ... M1... Cuerda 2 ... M2
Vcuerda 1 = V(M1 g / 0.00331) .................................V cuerda 2 = V( M2g / 0.00487)
Si las velocidades deben ser coincidentes tendras:
M1 / 0.00331 = M2 / 0.00487 ............................................0.00487 M1 - 0.00331 M2 = 0
y ademas ............................................................................M1 + M2 = M= 0.511
Resolves este sistema de 2 x 2 y estas llegando a que: M1 =0 .2068 Kg y M2= 0.3042 Kg.
