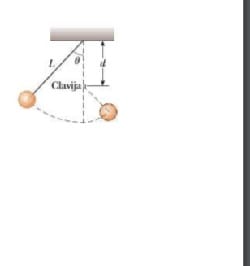
15. Un péndulo integrado por una cuerda de longitud L y una esfera, oscilaen un plano vertical. La cuerda golpea una clavija lo
¿Cómo están? Disculpen no se como hacer este ejercicio,¿podrían ayudarme? No logro comprender el dibujo, si hay alguna forma de que puedan explicármelo se los agradeceré!
15. Un péndulo integrado por una cuerda de longitud L y una esfera, oscila en un plano vertical. La cuerda golpea una clavija localizada a una distancia de debajo del punto de suspensión. Determinar la velocidad de la esfera en el punto más bajo de la trayectoria. Demostrar que si el péndulo se suelta desde la posición horizontal (=90°) y oscila en un círculo completo centrado en la clavija, entonces la distancia de es como mínimo 3/5 L.
Respuesta de Dario Costes
1
1 respuesta más de otro experto
Respuesta de albert buscapolos Ing°
1