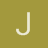Un reloj de péndulo simple .

a. (i) Escribir la ecuación diferencial que permitiría describir el movimiento del péndulo de longitud l ( inextensible sin masa) y una masa oscilante m puntual.

El movimiento es de rotación en torno de un punto fijo. El péndulo ideal de longitud l oscilará simétricamente alrededor de la vertical que pasa por el punto de suspensión.

La segunda Ley de Newton se expresaría aqui;

I d^2 ϑ / dt = - m g l senϑ ... El peso de la masa oscilante se descompone vectorialmente en una fuerza en direccion del hilo de suspension + una fuerza normal al eje de suspension, que vale mg sen ϑ.

(Ii) Plantear una solución considerando oscilaciones muy pequeñas.

Si las oscilaciones son pequeñas ( menores a 6 ° ) se puede aproximar suficientemente sen ϑ a

Θ ... con lo cual la ecuación quedaría: I d^2 ϑ / dt = - m g l ϑ que es la relación representativa del movimiento armónico simple.

Esta ecuacion tiene por solucion ;   ϑ   (t) = A cos ( w t - α )

A = Amplitud angular

l = longitud del péndulo

m = masa oscilante ( puntual)

w= pulsacion = frecuencia angular = ( l/g)^1/2

El periodo de oscilacion= constante= 2pi/w

(Iii) Luego de un minuto de viaje, que tiempo se adelanta o se atrasa el reloj.

Considerando el tiempo como invariable ( muy aceptable para las velocidades que puede alcanzar un ascensor en descenso) tienes que:

Al encontrarse en descenso, la aceleración que experimenta el reloj será la diferencia

( G - a), con lo cual el periodo variará según:

T (dentro del ascensor en descenso) = 2pi / ( l / (g-a))^0.5 seg.

T ( dentro del ascensor detenido ) = 2 pi/ ( l/ g)^0.5 seg

Relacionando ambos periodos con el lapso que te dicen tendrías el atraso real .

(¿Iv) Existe un valor de a para el que el reloj se detiene?

Si, Se detiene cuando esta en caída libre, es decir a = g.

¡Gracias! 

w= pulsacion = frecuencia angular = ( l/g)^1/2 pero la formula no es ( g/l)^1/2

Y al calcular el punto III) Y IV) también cambiaría o como se analiza que w= ( l/g)^1/2 

Perdon, escribi erroneamente una parte : Rectifico:

w= pulsacion = frecuencia angular = ( l/g)^1/2 

Periodo = 2pi w = 2pi  ( l/g)^1/2 

Claro, en los puntos iii y iv no se divide sino que se multiplica por la pulsación.

Correcta tu observación.

Me puedes ayudar como quedaría en punto Iv para ver como calcular la aceleración.

No... no tienes que calcular nada, Fíjate que cuando a = g el periodo

T = 2pi ( l (g-a))^0.5 seg. = 0 ..........con lo cual tu pendulo queda inmovil.

Pero el periodo no es algo así:

T= 2pi ( l/(g-a))^1/2  y si a=g es obtendría un cero en el denominador o como se obtiene que la l multiplique a g-a