Calcula e interpreta el resultado
justificando
$$\int_{-5}^4 |3x+9| dx$$(realiza la representación gráfica de dicho recinto)
1 respuesta
Hacemos primero el dibujo y nos daremos cuenta de todo.
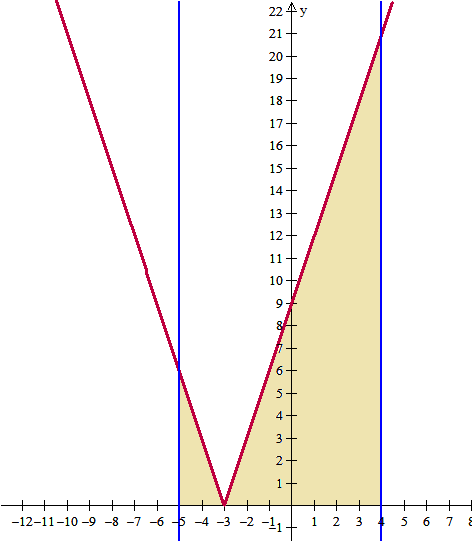
Se ve que en (-oo,-3) la función 3x+9 es negativa y (3x,+oo) es positiva. Debemos dividir el dos trozos el intervalo de integración y sumar las áreas de los dos.
El intervalo (-5, -3) nos dará área negativa. O le cambiamos el signo después o cambiamos antes el signo de la función. Yo voy a cambiarlo mejor después y así la misma integral indefinida me sirve para los dos trozos.
Vamos por tanto a hacer la integral indefinida de 3x+9, es directa, asi que la escribimos ya
Int = 3x^2/2 + 9x
entre -5 y -3 es
27/2 - 27 - 75/2 + 45= 18 - 48/2 = (36-48)/2 = -6
Área izquierda = 6
y entre -3 y 4 es
24 + 36 - 27/2 + 27 = 87 - 27/2 = (174 -27)/2 = 147/2
Área derecha = 147/2
Luego el área total es
6 + 147/2 = (12+147)/2 = 159/2
Y eso es todo.
