,Por el diámetro calcular metros de un rollo

He aquí el dibujo de como irá más o menos el rollo. No salió muy bien pero supón que las dos vueltas tiene el mismo grosor.

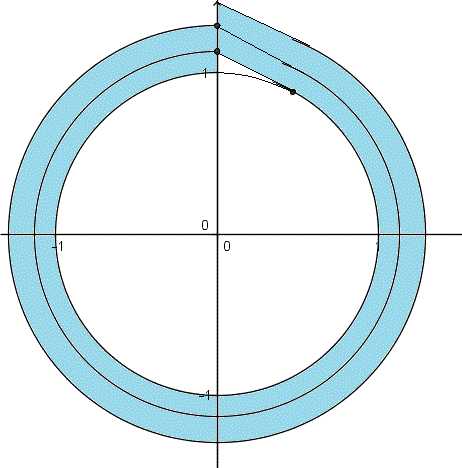
Como puedes ver hay un trozo en que en vez de ser circular se supone que el rollo sigue una línea recta.

El cáculo de esa distancia recta es un problema bastante complicado. Entonces lo que se puede hacer es considerar que el rollo está formado por circulos concentricos. Si ekl diametro es grande y el grosor pequeño tan apenas se comete error haciendo esa sustitución. Y ademas va a resultar una fórmula mucho más sencilla.

Haremos mejor las cuentas con los radios que serán 25mm y 300mm

La diferencia es 275 mm. No es una buena diferencia, porque las vueltas son esa distancia dividida entre los 2 mm de grosor y no nos va a dar un número entero de vueltas.

Las vueltas serán 137 o 138

Para compensar lo que vamos a perder por no poner esos tramos de recta, vamos a tomar para cada círculo concéntrico el radio más exterior que dará más medida que si tomamos el interno o el medio

Asi el primer radio sería 27, el siguiente 29, 31, etc

El radio de la vuelta 137 será

27+2·136= 299

La suma de las longitudes de las cincunferencias de las 137 vueltas será

longitud rollo(137) = 2·Pi·(27+29+31+...+299)

En el paréntesis tenemos una sucesión aritmetica. La suma de n términos de una sucesión aritmética es

Sn= (a1+an)n/2

con lo que tenemos

lontitud rollo(137) = 2Pi(27+299)·137/2 = Pi(226)137=30962·Pi mm

Longitud rollo(137) = 97270 mm = 97.27 m

Como decíamos que estaba mal el diámetro del rollo porque no se adaptaba a un número entero de vueltas, cacularemos también la longitud con 138 vueltas

Longitud rollo(138) = 97270+2·Pi·301 = 99161 mm = 99,161 m

Toma la longitud que quieras de las dos o la intermedia,

97,27 m

99,161 m

98.2155 m

Cuando tengamos un rollo que realmente tenga un número entero de vueltas, llamemos R al radio total y r al del canuto y g al grosor y la fórmula será:

Longitud = Pi(r+g+R)(R - r)/g

Y eso es todo.