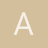Formula para calcular el peso de un tubo de carton

El peso puede variar bastante en función del grosor del cartón y el número de vueltas. Si fuese un tubo de diámetro pequeño con muchas vueltas habrá bastante diferencia entre la longitud de la primera y última vuelta. Mientras que si es un tubo de mucho diámetro con espesor pequeño no hay prácticamente diferencia entre las vueltas.

Luego voy a añadir la variable g que será el grosor del cartón para que salga más exacto. Y por diámetro voy a entender el diámetro externo.

La longitud de cada vuelta se tomará aproximadamente por el punto medio del grosor del cartón

Así la ultima vuelta necesita:

$$\begin{align}&\left(d-\frac g2\right)\pi\\ &\\ &\text {la penultima necesita}\\ &\\ &\left(d-g-\frac g2\right)\pi =\left(d-\frac {3g}2\right)\pi\\ &\\ &\text{Y si son n vueltas la primera necesita}\\ &\\ &\left(d-(n-1)g-\frac g2\right)\pi=\left(d-\frac {(2n-1)g}2\right)\pi\\ &\\ &\\ &\text{La suma de todas las vueltas es:}\\ &\\ &l=nd\pi-\frac{g\pi}{2}[1+3+5+ ··· + (2n-1)]=\\ &\\ &\text{Y por la fómula de suma de sucesiones aritméticas}\\ &\\ &\\ &l=nd\pi-\frac{g\pi}{2}·\frac{n(1+2n-1)}{2}\\ &\\ &\\ &l=nd\pi-\frac{g\pi n^2}{2}\\ &\\ &\\ &l=n\pi\left(d-\frac{ng}{2}  \right)\end{align}$$

Y esa es la longitud más o menos. Puede que sea un poquito más porque donde se juntan las vueltas no hay circunferencias perfectas sino que al montar una sobre otra hay un poco más de longitud. Y dependiendo de la elasticidad del material también puede cambiar un poco.

Se puede calcular un límite inferior y superior para saber el error que se puede cometer, consiste en hacer las cuentas anteriores con -g y 0 en lugar de -g/2

Hechas esas cuentas se obtiene un intervalo en la solución de radio n·Pi·g/2,

$$l=n\pi\left(d-\frac{ng}{2}  \right)\pm \frac{n\pi g}{2}$$

Entiéndase que la fórmula es lo primero que lo que viene después con más menos solo es la estimación máxima del error.

Y eso es todo, espero que te sirva y lo hayas entendido. SI no es así pregúntame. Y si ya está bien no olvides puntuar, para poder hacer futuras preguntas.

Antes que nada mil gracias por ayudarme. para ejemplificar la pregunta quiero aclararles que a modo de ejemplo, yo tengo en mi poder un tubo de cartón que ya fabricamos y obviamente lo puedo pesar una vez terminado y asi obtener el peso del mismo, pero lo que necesito es saber el peso del mismo antes de fabricarlo, en este caso es un tubo de cartón en le que se utiliza un cartón de 300grs y para formar las paredes del tubo se necesitan 5 vueltas de ese cartón de 300gr ahora bien este tubo tiene un diámetro exterior de 8,5 cms y sus paredes tienen un espesor de 5mm el alto del tubo es de 93mm como yo lo tengo en mis manos como dije antes lo peso y pesa 70grs que formula debo aplicar para obtener ese resultado.otra vez mil gracias por la ayuda que me puedan brindar.

Había hecho el cálculo de la longitud de cartón, luego había que calcular el área multiplicando por el alto del tubo y finalmente el peso.

Para que está fórmula funcione el tubo tiene que estar muy bien hecho sin holgura entre las sucesivas vueltas de cartón. Eso puede ser un poco difícil con un espesor de 5mm (medio centímetro) si no se hace con máquinas. Las cuentas serían:

$$\begin{align}&l=n\pi\left(d-\frac{ng}{2}  \right)\\ &\\ &\\ &l=5\pi\left(85-\frac{5·5}{2}  \right)=362.5\pi=1138.8273mm\\ &\\ &Area= 93\times 362.5\pi = 105910.94; mm^2\\ &\\ &\text{Traducido a }m^2\\ &\\ &Area = 0.10591094 m^2\\ &\\ &Peso = 300 \times 0.10591094 = 31.77 g \\ &\\ &\\ &\end{align}$$

Como puedes ver no se parece en nada. Mira a ver si están bien los datos, si el peso es gramos por metro cuadrado, y si los 8.5 cm son el diámetro exterior o el interior.

Compara también la longitud del cartón del tubo, mira a ver si se parece a los 1138 mm que digo yo. Aunque los datos sean correctos tiene que estar muy bien hecho el tubo para que dé eso.