Problema sobre puntos cardinales?

Hay un pequeño error en el enunciado. A los 5 minutos dices que la torre P esta SO y O-SO

Es la torre M la que está O-SO tal como puedes ver en la figura.

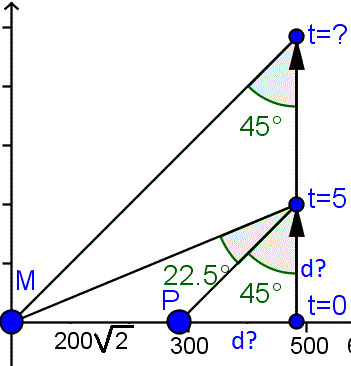
Una vez hecho el dibujo el resto es relativamente fácil. Tomamos el ángulo suma de los dos que confluyen en el tiempo t=5. Es un ángulo de 67.5º

La tangente de este angulo será el cateto opuesto entre el adyacente

$$\begin{align}&tg\;67.5º=\frac{d+200 \sqrt 2}{d}\\ &\\ &2.414213562=\frac{d+200 \sqrt 2}{d}\\ &\\ &2.414213562·d=d+200 \sqrt 2\\ &\\ &2.414213562·d-d=200 \sqrt 2\\ &\\ &1.414213562·d=200 \sqrt 2\\ &d = \frac{200 \sqrt 2}{1.414213562}=200 \;m\end{align}$$

Al ser 45º el ángulo cuando llega al final los catetos son iguales y le queda por recorrer

$$\begin{align}&200 \sqrt 2 \;m\\ &\\ &\text {Si 200 m le costaron 5 min, ahora necesitará:}\\ &\\ &5 \sqrt 2\; minutos = 7.071067812\;min =7\;min\;4.26\;seg\end{align}$$

Y ESO ES TODO. Ahora te dejo para nota la curiosidad sobre que la calculadora diese como tangente de 67,5º algo tan parecido a 1+raíz de 2. No es sencillo, si no lo entiendes tampoco te rompas la cabeza.

$$\begin{align}&tg \left( \frac a2 \right )=\sqrt{\frac{1-cosa}{1+sena}}\\ &\\ &\\ &tg(22.5º)= tg \left (\frac{45º}{2} \right )=\frac{\sqrt{1-\frac{\sqrt 2}{2}}}{\sqrt{1+\frac{\sqrt 2}{2}}}=\frac{\sqrt{2-\sqrt 2}}{\sqrt{2+\sqrt 2}}\\ &\\ &\\ &tg(a+b)=\frac{tga+tgb}{1-tga·tgb}\\ &\\ &tg(67.5º)=tg(45º+22.5º)=\\ &\\ &\\ &\frac{tg45º+tg22.5º}{1-tg45º·tg22.5º}=\\ &\\ &\frac{1+tg22.5º}{1-tg22.5º}= \frac{(1+tg22.5º)^2}{1-tg^2\,22.5º}=\\ &\\ &\\ &\frac{\left ( 1+\frac{\sqrt{2-\sqrt 2}}{\sqrt{2+\sqrt 2}} \right )^2}{1-\frac{2-\sqrt 2}{2+\sqrt 2}}=\frac{(\sqrt{2+\sqrt 2}+\sqrt{2-\sqrt 2})^2}{2+ \sqrt 2-2+\sqrt 2}=\\ &\\ &\\ &\frac{2+\sqrt 2+2-\sqrt 2+2 \sqrt{(2+\sqrt 2)(2-\sqrt 2)}}{2 \sqrt 2}=\\ &\\ &\\ &\frac{4+2 \sqrt{4-2}}{2 \sqrt 2}=\frac{2+\sqrt 2}{\sqrt 2}=\\ &\\ &\\ &1+\frac{2}{\sqrt 2}= 1+\frac{2 \sqrt 2}{2}=1+\sqrt 2\\ &\\ &\\ &Resumiendo\\ &\\ &tg\;67.5º= 1 + \sqrt 2\end{align}$$

¡Uff! Pero como te decía, esta parte final simplemente sirve para no utilizar la calculadora, te la puedes saltar si ves que supera el nivel de tus estudios.

Y eso es todo.