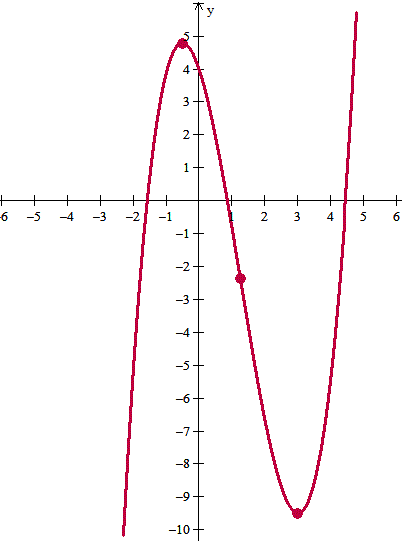Puntos Críticos, Inflexión, Intervalos... De una Función
¿Me podrías colaborar con la siguiente pregunta?
Muchas gracias de antemano.
Dada la función:
1. Determine los puntos críticos de la función.
2. Determina los intervalos donde la función es creciente, decreciente o constante.
3. Encuentra los puntos de inflexión.
4. Determina los intervalos de concavidad.
5. Encuentra los puntos máximos relativos y mínimos relativos de la función.
6. Finalmente, traza la gráfica que cumple con las condiciones establecidas en los puntos anteriores.
1 Respuesta
1) Los puntos críticos son los que la derivada vale 0
f'(x) = 2x^2 - 5x - 3 = 0
x = [5 +- sqrt(25+24)]/4 = (5 +- 7)/4 = 3 y -1/2
2) La derivada es un polinomio de grado dos con dos respuestas y coeficiente positivo en x^2, es por tanto una parábola en forma de U que sera positiva en lo extremos y negativa en la zona entre las raíces
creciente en (-oo, -1/2) U (3, +oo)
decreciente en (-1/2, 3)
3) Los puntos de inflexión son los ceros de la derivada segunda siempre que la próxima no nula sea impar.
f ''(x) = 4x - 5 = 0
4x = 5
x = 5/4
y f '''(x) = 4 luego no es nula en x=5/4 y es punto de inflexión
4) La derivada segunda es una recta con pendiente positiva, luego será negativa hasta cortar el eje y después positiva
Es cóncava hacia abajo en (-oo, 5/4)
Es cóncava hacia arriba en (5/4, +oo)
5) Un polinomio de grado si tiene dos puntos críticos tiene primero el máximo y después el mínimo. Puedes verlo porque primero es creciente hasta el primer punto critico, luego decrece hasta el segundo y después vuelve a crecer.
También puedes usar el criterio de la derivada segunda
f ''(-1/2) =4(-1/2)-5 =-2-5 = -7
Al ser negativa es un máximo
f ''(3) = 4·3-5 = 7
al ser positiva es un mínimo
Luego x=-1/2 es un máximo y x=3 es un máximo.
6) Calculamos los valores de la función en los puntos que hemos hallado
f(-1/2) = (2/3)(-1/2)^3 - (5/2)(-1/2)^2 - 3(-1/2) + 4 =
-2/24 - 5/8 + 3/2 + 4 = (-2 - 15 + 36 + 96)/24 = 115/24
Máximo en (-1/2, 115/24) aprox (-0.5, 4.791666...)
f(-3)= (2/3)27 -(5/2)9 - 9 + 4 =
18 - 45/2 - 9 + 4 = 13-45/2 = (26-45)/2 = -19/2
Mínimo en (3, -19/2) = (3, -9.5)
f(5/4) = (2/3)(125/64) -(5/2)(25/16) - 15/4 + 4 =
250/192 -125/32 - 15/4 + 4=
(250 - 750 - 720 + 768) / 192 = .-452/192 = -113/48
Punto de inflexión en (5/4, -113/48) aprox (1.25, 2.354166...)
Y si es preciso se evalúa la función en algún punto más para hacer la gráfica, el (0,4) sale automático y los otros que quieras los evalúas.
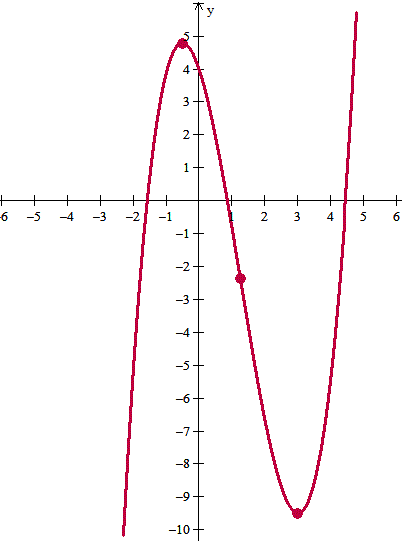
Y eso es todo.
¡Que bien, entonces mi desarrollo del último ejercicio del parcial está perfecto!
Muchas gracias valeroasm por tomarse el tiempo de hacer este ejercicio tan extenso, no se que haría sin ti en matemáticas. Eres todo un maestro.
