Estudiar función f(x)= 6x / x^2 + 1

1) El Dominio es todo R ya que el denominador no se anula nunca

x^2+1= 0

x^2 = -1 No tiene respuestas reales

2) El único punto de corte con el eje X es 0 que anula el numerador y el punto es

(0,0)

Y con el eje Y tiene ese mismo corte

3) Tiene simetría central, es una función impar.

Ya que f(-x) = -f(x)

4) No tiene asíntotas verticales

Tiene asíntotas horizontales iguale en -infinito y +infinito ya que el límite de f(x) en los infinitos es 0

Luego la asíntota horizontal es la recta y=0, el eje X.

Y por tener horizontales no tiene oblicuas

5) Para hallarlos habrá que hacer la derivada

$$\begin{align}&f(x) = \frac{6x}{x^2+1}\\ &\\ &\\ &f'(x) = \frac{6(x^2+1)-6x(2x)}{(x^2+1)^2}=\\ &\\ &\\ &\frac{6x^2+6-12x^2}{(x^2+1)^2}= \frac{ 6(1-x^2)}{(x^2+1)^2}\end{align}$$

Los ceros de la derivada primera son

1-x^2 = 0

x^2 = 1

x = -1 y 1

En (-oo, -1), por ejemplo -2 el signo de la derivada es [1-(-2)^2] = -3 la función decrece

En (-1,1) por ejemplo en 0 el signo será (1 -0^2) = 1 la función es creciente

En (1,+oo) poe ejemplo en 2 el signo es (1-2^2) = -3 la función es decreciente

6) Los puntos críticos eran -1 y 1

Ya vimos que hasta -1 la función decrecía y luego crecía, luego en x=-1 hay un mínimo y el punto es

(-1,-6/[(-1)^2+1]) = (-1, -6/2) = (-1, -3)

Y vimos que hasta el 1 va creciendo y luego decrece, luego es un máximo que se calcula es

(1,3). Tiene que existir y ser ese por motivo de la simetría central de la función.

7) Para la concavidad hacia arriba o hacia abajo (porque hablar de concavidad y convexidad es como la torre de Babel) se tiene que calcular la derivada segunda

$$\begin{align}&f'(x)=\frac{ 6(1-x^2)}{(x^2+1)^2}\\ &\\ &\\ &\\ &f''(x)=6\left( \frac{-2x(x^2+1)^2-(1-x^2)2(x^2+1)2x}{(x^2+1)^4} \right)=\\ &\\ &\\ &\\ &6\left(\frac{-2x(x^2+1)-4x(1-x^2)}{(x^2+1)^3}\right)=\\ &\\ &\\ &6\left(\frac{-2x^3-2x-4x+4x^3)}{(x^2+1)^3}\right)=\\ &\\ &\\ &6\left(\frac{2x^3-6x}{(x^2+1)^3}\right)= 12 \left(\frac{x^3-3x}{(x^2+1)^3}\right)\end{align}$$

Los ceros son

x^3 - 3x = 0

x=0

x^2 - 3 = 0

x = +- sqrt(3)

luego hay tres raíces -sqrt(3), 0, sqrt(3)

Calculamos el signo de la derivada segunda en cada uno de los tres intervalos que se forman, si es positiva se llamara cóncava hacia arriba (cóncava en España y convexa en EEUU) y si es negativa será cóncava hacia abajo (convexa en España y cóncava en EEUU). Por eso que mejor lo de cóncava hacia abajo o arriba. Cóncava hacia arriba significa que tiene forma de U. A lo mejor a ti te han enseñado ya con el sistema anglosajón porque al final se imponen en todo, pero a mí me enseñaron con el que digo.

El signo de la derivada segunda queda determinado por x^3-3x

En (-oo, -sqrt(3)) en -2 por ejemplo -8 +6 = -2 es cóncava hacia abajo

En (-sqrt(3), 0) en -1 por ejemplo -1+3 = 2 es cóncava hacia arriba

En (0, sqrt(3) es cóncava hacia abajo, puedes calcularlo pero yo lo digo porque la simetría central cambia el tipo de concavidad

En (sqrt(3), oo) es cóncava hacia arriba por simetría central con (-oo, -sqrt(3))

Esta es la gráfica donde puse los puntos de inflexión

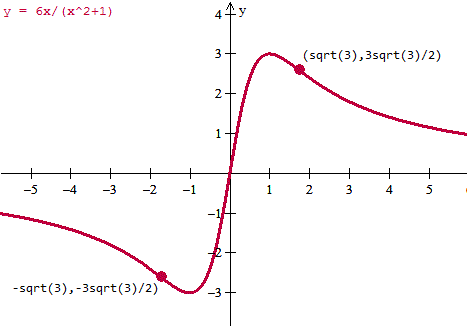
8) Y los puntos de inflexión son los ceros de la derivada segunda ya calculados, los puntos con las dos coordenadas son:

(-sqrt(3), -6sqrt(3)/(3+1)) = (-sqrt(3), -(3/2)sqrt(3))

(0,0)

(sqrt(3), 6sqrt(3)/(3+1)) = (sqrt(3), (3/2)sqrt(3))