Hallar el volumen generado en la rotación del área comprendido por las funciones Y=-x2-3x+6

Recuerdo que la gráfica era esta. Esta vez toca rotar sobre la recta x=3.

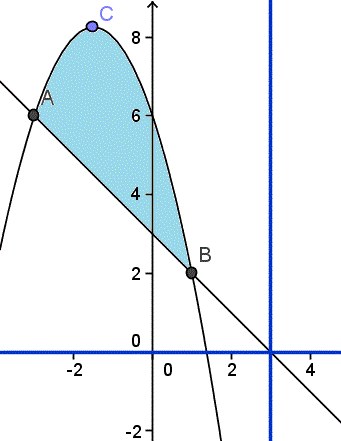
Lo primero copio cálculos que ya se hicieron en la otra parte

Calculamos los puntos A, B y C.
y = -x^2 - 3x + 6
y = 3-x
-x^2 - 3x + 6 = 3-x
x^2 + 2x - 3 = 0
xa=-3; xb= 1
A=(-3, 6)
B=(1,2)
C es el vértice de la parábola
xc= -b/2a = 3/(-2) = -3/2
yc= -9/4 + 9/2 + 6 = 6+9/4 = 33/4
C=(-3/2, 33/4)

Ahora haremos el cambio de variable que haga que la recta x=3 sea el eje Y nuevo

Tenemos

x vieja = x nueva + 3

sustituimos las x viejas por x+3

Y=-x^2-3x+6

Y = -(x+3)^2 - 3(x+3) +6 = -x^2 - 6x - 9 - 3x - 9 +6 = - x^2 - 9x -12

Siempre queda la duda de si era ese el cambio o el contrario, lo comprobaremos con un punto. El punto B por ejemplo, antes era (1,2) ahora la coordenada x será -2 tal como se ve en el dibujo, veamos cuanto vale Y

-(.2)^2 -9(-2)-12 = -4 + 18 -12 = 2

lo que tenía que valer, la prueba confirma que el cambio se hizo bien.

Y las nuevas coordenadas serán

A = (-6,6)

B = (-2,2)

C = (-9/2, 33/4)

Y coma la rotación va a ser respecto al nuevo eje Y hay que poner la ecuación en función de y

x = g(y)

Que además van a ser dos funciones, el ejercicio es completo.

Como

y = -x^2 -9x -12

x^2 + 9x +12 + y =0

despejamos x

x=[-9 +-sqrt(81-48-4y)] / 2

x = [-9+-sqrt(33-4y)]/2

La rama derecha (la que contiene el punto B) es la que tiene valores de x más altos, luego es

$$\begin{align}&Derecha: \; x=\frac{-9+\sqrt{33-4y}}{2}\\ &\\ &\\ &\\ &Izquierda: x=\frac{-9-\sqrt{33-4y}}{2}\end{align}$$

Y también tenemos que poner en coordenadas nuevas la recta

x+y-3=0

Cambiamos x por x+3

x+3+y-3 = 0

x+y = 0

x=-y

Que está bien tal como puede verse en la gráfica

Pues ya ha llegado el momento de plantear las integrales:

La parte más externa (que dará el volumen de la figura compacta) está formada por la recta y parábola izquierda f y a ese volumen habrá que restar el hueco central que es volumen generado por la otra rama de la parábola.

Volumen completo = (Volumen generado por la parábola izquierda entre A y C) + (Volumen generado por la recta entre B y A) - (Volumen generado por la rama derecha entre B y C

$$\begin{align}&\pi \int_6^{33/4}(-9-\sqrt{33-4y})^2dy+\\ &\\ &\\ &\\ &\pi \int_2^6 y^2dy- \\ &\\ &\\ &\\ &\pi \int_2^{33/4} (-9+\sqrt{33-4y})^2dy=\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\pi \int_6^{33/4}(81+33-4y+18 \sqrt{33-4y})dy +\\ &\\ &\\ &\pi \left [ \frac{x^3}{3} \right ]_2^6 -\\ &\\ &\\ &\pi \int_2^{33/4}(81+33-4y-18 \sqrt{33-4y})dy=\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\left [ 114y - 2y^2 -3(33-4y)^{3/2} \right ]_6^{33/4}+\\ &\\ &\\ &\pi \left [ \frac{x^3}{3} \right ]_2^6 -\\ &\\ &\\ &\pi \left [ 114y - 2y^2 +3(33-4y)^{3/2} \right ]_2^{33/4}=\\ &\\ &\\ &\\ &\\ &\\ &\\ &\pi \left [ \frac{114·33}{4} -\frac{2·(33)^2}{16}-3·0-114·6 +2·6^2+3·27 \right ]+\\ &\\ &\\ &\pi \left [ \frac{6^3}{3} - \frac{2^3}{3} \right ]-\\ &\\ &\\ &\pi \left [ \frac{114·33}{4} -\frac{2·(33)^2}{16}-3·0-114·2 +2·2^2-3·125 \right ]=\end{align}$$

Simplificaremos algunos sumandos del primer y tercer grupo que son iguales con signo opuesto e iremos realizando operaciones

$$\begin{align}&\pi \left [-684 +72+81 \right ]+\pi \left [ 72 - \frac{8}{3} \right ]-\pi \left [-228 +8-375 \right ]=\\ &\\ &\pi(-531+72-\frac{8}{3}+595)=\\ &\\ &\pi \left ( 136-\frac{8}{3} \right )= \\ &\\ &\\ &\frac{400 \pi}{3}\end{align}$$

Y eso es todo.