Integral triple en el primer octante

No es nada fácil el problema. Seguramente se puede hacer sin la gráfica pero mejor hacerla.

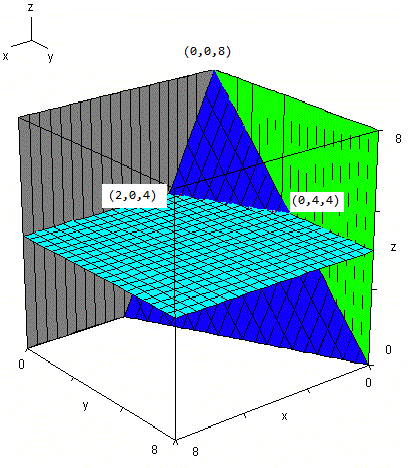
Es la pirámide que queda en la parte de arriba

La recta (2,0,4) a (0,4,4) referida al plano XY y con ambas variables despejadas es

(x-2)/(-2) = y / 4

y = -2x+4

x = 2 - y/2

Con esto tenemos estas dos formas

$$\begin{align}&1) \quad\int_0^2\int_0^{-2x+4}\int_4^{8-2x-y}dz\,dy\,dx\\ &\\ &\\ &2) \quad \int_0^4\int_0^{2-\frac y2}\int_4^{8-2x-y}dz\,dx\,dy\end{align}$$

Ahora hagamos que y sea la primera que se integra, entonces se integra entre el plano y=0 y el plano z = 8 - 2x - y pero vamos a ponerlo en función de y, será

y = 8 - 2x - z

La recta que nos interesa ahora es la que esta en en plano y=0 que es la que une los puntos

(0,0,8) y (2,0,4)

x / 2 = (z-8) / (-4)

-4x = 2z - 16

y las dos forma de expresarla son

z = 8 - 2x

x = 4 - z/2

con lo cual tenemos estas dos integrales

$$\begin{align}&3)\quad\int_0^2\int_0^{8-2x}\int_0^{8-2x-z}dy\,dz\,dx\\ &\\ &\\ &\\ &4) \quad\int_4^8\int_0^{4-\frac z2}\int_0^{8-2x-z}dy\,dx\,dz\end{align}$$

Y finalmente hagamos que se la x la primera que se integra

Se integrará entre el plano x= 0 y el plano expresado en función de la x que es

x=(8-y-z)/2

La recta que limitará el dominio de la base es la que está en el plano x=0, que pasa por los puntos

(0,0,8) y (0,4,4)

y / 4 = (z-8) / (-4)

y = 8 - z

z = 8 - y

Y tendremos estas dos integrales

$$\begin{align}&5)\quad \int_0^4\int_0^{8-y}\int_0^{\frac{8-y-z}{2}}dx\,dz\,dy\\ &\\ &\\ &\\ &6)\quad \int_4^8\int_0^{8-z}\int_0^{\frac{8-y-z}{2}}dx\,dy\,dz\end{align}$$

Y eso es todo, interesante problema pero hay que tener los 5 sentidos puestos para entenderlo y no equivocarse.