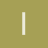Calcular la autovalores de la aplicación lineal

a)

Primero calculamos la matriz de la aplicación lineal respecto a la base canónica. Es esta:

|2  1  0|
|0  1 -1|
|0  2  4|

Basta multiplicar por (x,y,z)T para ver que obtenemos la aplicación lineal lineal.

Los autovalores son las raíces del polinomio característico:

|2-t  1    0|
|0   1-t  -1| = 0
|0    2  4-t|

(2-t)(1-t)(4-t)+2(2-t) =0

(2-t)[(1-t)(4-t)+2] = 0

Luego el primer valor propio es t=2 y calculamos las raíces del corchete

4-t-4t+t^2+2 = 0

t^2-5t +6 = 0

t = [5+-sqrt(25-24)]/2 = (5+-1) = 2 y 3

Luego en resumen tenemos los valores propios

t = 2 con multiplicidad 2

t = 3

b) Ahora hemos de calcular los vectores propios:

Esto podrás ver varias formas de hacerlo. Me atendré a la definición que dice que X es un vector propio correspondiente al valor propio t si

(A-tI)X = 0

Encontrar X es halar la solución de una ecuación homogénea cuya matriz de coeficientes es A-tI

Resolvemos para t = 3 lo primero

       -1  1  0
A-3I =  0 -2 -1
        0  2  1
La segunda y tercera filas son proporcionales solo sirve una 
y las respuestas serán infinitas

Si tomamos z como parámetro tendremos

-2y - z = 0

-2y = z

y = -z/2

Y la primera ecuación sera

-x+y = 0

x = y = -z/2

Luego la solución es (-z/2, -z/2, z) para todo z € R

Podemos expresarla más cómodamente como (z, z, -2z) para todo z€R

Esto es, el subespacio de los autovectores asociados al valor propio t=3 tiene dimensión 1 y su base es:

B3={(1, 1, -2)}

Ahora calculamos el subespacio de autovectores para el valor propio 2

0  1  0
0 -1 -1
0 2 2

La segunda y tercera fila son proporcionales luego sobra una y habrá infinitas soluciones.

X puede tomar cualquier valor como en todas las ecuaciones tiene coeficiente cero no sumará nada, lo tomamos como parámetro

y = 0

-y -z = 0

z = -y =0

Luego la solución es (x, 0,0) para todo x€ R.

Es un espacio vectorial de dimensión 1 y su base es

B2={(1, 0, 0)}

c) No es diagonalizable porque no hay tres vectores propios linealmente independientes, debería haber sido uno de los dos subespacios de dimensión 2.

Y eso es todo.

Hola Experto!!

Hay 2 pasos del problema que no termino de entender. He estado mirándome mis apuntes a ver si lo sacaba y nada...

1) ¿Qué es lo que se hace en este paso? :

(2-t)(1-t)(4-t)+2(2-t) =0

(2-t)[(1-t)(4-t)+2] = 0

¿De dónde sale ésto?:

t = [5+-sqrt(25-24)]/2 = (5+-1) = 2 y 3

2) ¿Qué se hace para expresar (-z/2, -z/2, z) como (z, z, -2z)?

A la espera de su respuesta,

Muchas gracias y Un Saludo!!

1) Lo primero

(2-t)(1-t)(4-t)+2(2-t) =0
(2-t)[(1-t)(4-t)+2] = 0

Es que he sacado factor común (2-t)

Lo segundo es la resolución de la ecuación de segundo grado:

t^2-5t +6 = 0

Y lo q
t = [5+-sqrt(25-24)]/2 = (5+-1) = 2 y 3

Espera, que se mando sola la respuesta cuando no había terminado.

Repetimos parte.

Lo segundo es la resolución de la ecuación de segundo grado:
t^2 - 5t + 6 = 0
Que se hace con la fórmula habitual, lo que quizá no entiendas es que sqrt significa raíz cuadrada. Es la forma internacional de designarla. Y las dos soluciones son:

t = [5+-sqrt(25-24)]/2 = (5+-1)/2 = 2 y 3

Veo que se me olvidó poner el denominador 2 en la segunda igualdad, ahora está bien.

2) El espacio vectorial formado por los vectores de la forma (-z/2, -z/2, z) para todo z€R

Es el mismo que el formado por los vectores (z, z, -2z) para todo z€ R.

El primero se genera como combinaciones lineales del vector (-1/2, -1/2, 1) y el segundo como combinaciones lineales de (1,1,-2).

Pero es que el uno es combinación lineal del otro, o sea, que generan el mismo espacio vectorial. Basta multiplicar el primero por (-2) y tienes el segundo.

Estas dudas que tenías son cosillas que yo entiendo son de un nivel bastante mas elemental que la dificultad que tiene el estudio de los valores y vectores propios, la diagonalización de matrices, etc. Tendrías que repasar estudios anteriores.

Efectivamente, en la primera parte lo que no entendía era que significaba "sqrt", siento no haberme explicado mejor. Así mismo, también sabía que aquí: (2-t)[(1-t)(4-t)+2] = 0 se estaba sacando factor común, lo que no entiendo es por qué se le suma 2 al final.

A la espera de su respuesta,

Gracias de antemano y disculpe las molestias!!

Es la propiedad distributiva del producto que dice

a(b+c) = ab + ac

Si lo que nos dan es

ab + ac

el sacar factor común es ponerlo en la forma

a(b + c)

Lo que queda dentro del paréntesis es lo que "sobra" de a en los productos ( en realidad habría que decir el cociente entre a)

Si nosotros teníamos:

(2-t)(1-t)(4-t) + 2(2-t)

Al sacar factor común (2-t) el cociente del primer sumando entre (2-t) es (1-t)(4-t) y el segundo es 2; por lo tanto, por analogía con lo que te enseñe con las letras queda:

(2-t) [(1-t)(4-t) + 2]