Se dobla la esquina superior izquierda de un trozo de papel de 8 cm ancho por 12 cm de largo para

Las palabras largo y ancho son equivalentes en un rectángulo. Sería mejor si usaras las palabras base y altura y me dices cuál es cada una

asi decía el enunciado del taller que me dejaron, pero según lo que le entendí al profesor 12 es la base y 8 la altura

gracias por su ayuda

No sé si lo habré entendido bien.

La esquina superior izquierda puede ir a parar a cualquier punto del lado derecho.

Lo que hay que minimizar es la línea por la que se dobla.

Experimentalmente he comprobado que la doblez siempre va desde el lado superior hasta el inferior del rectángulo, luego será más corta cuanto más vertical sea. Y se puede conseguir la vertical total si doblamos la esquina superior izquierda sobre la derecha (doblar por la mitad) donde la doblez medirá 8 cm.

Si he interpretado bien el problema esa sería la solución y si acaso haría falta demostrar que lo que vi experimentalmente es verdad.

Yo creo que a lo mejor sea al revés el problema, que la base sea 8 y la altura 12, eso si que da dobleces de arriba a izquierda junto con otras de arriba abajo y la solución no es tan elemental. ¿Crees qué debería hacerlo con esa forma?

yo copie tal cual el enunciado como me lo dieron pero según lo que me dijo el profesor es que la esquina izquierda de la hoja toque la parte inferior, eso forma un triangulo y lo que pide optimizar es, efectivamente, el doblez.

¡Uy qué lio!

Habría cuatro formas según la base sea 12 u 8 cm y según se leve la esquina izquierda al lado derecho o al lado de abajo. Pero son equivalente dos a dos. Voy a hacer el ultimo enunciado que dices con 12 de base y 8 de altura y llevando la esquina superior izquierda a la parte de abajo. Con esta y la anterior tendrás todos los casos estudiados.

Haré un dibujo para entenderlo mejor. Llamaremos x a la distancia a la que llevaremos la esquina superior izquierda al doblarla. En el dibujo será la distancia DX. Y llamaremos y a la distancia al punto de la izquierda por el que se dobla. En el dibujo será la distancia DY

Partiremos de que vamos a llevar la esquina superior izquierda a X, luego la variable que utilizaremos será x

La distancia AY debe ser igual a la distancia YX con eso podemos calcular Y, después él angulo alfa y por consiguiente el beta y con ello la distancia XG y al final la doblez que derivaremos para hallar su mínimo.

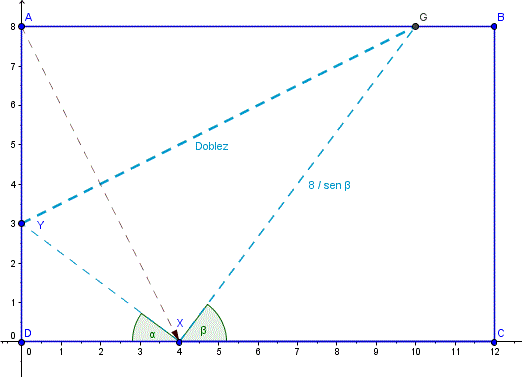
AY = YX ==> (8-y)^2=x^2+y^2 ==> 64-16y+y^2=x^2+y^2 ==> 64-x^2=16y ==> y=4-(x^2)/16

alfa y beta son complementarios luego

sen(beta)=cos(alfa)=x/sqrt(x^2+y^2)

XG = 8/sen(beta) = 8sqrt(x^2+y^2)/x

Doblez= sqrt(XY^2+XG^2) = sqrt[x^2+y^2+64(x^2+y^2)/x^2]

A la hora de calcular un mínimo se puede prescindir de la raíz cuadrada porque si el mínima la raíz también lo es el radicando. Formamos la función f sin el radical

f(x,y) = (x^2+y^2)(1+64/x^2)

Pensaba hacerla una función de una sola variable x, pero será más sencillo hacerla función de y. Para ello sabemos que

x^2+y^2=(8-y)^2

x^2 = 64-16y

con lo cual

f(x,y) = g(y) = (8-y)^2[1+64/(64-16y)] = (8-y)^2[1+ 4/(4-y)]

$$\begin{align}&g´(y)= -2(8-y)\left(1+\frac{4}{4-y}\right)+(8-y)^2 \frac{4}{(4-y)^2}=0\\ &\\ &\text {Un punto critico es y=8 pero no tiene sentido}\\ &\text{porque significa no doblar nada}\\ &\\ &-2\left(1+\frac{4}{4-y}\right)+(8-y) \frac{4}{(4-y)^2}=0\\ &\\ &\\ &-2\left(\frac{8-y}{4-y}\right)+\frac{4(8-y)}{(4-y)^2}=0\\ &\\ &\\ &\frac{-2(8-y)(4-y)+4(8-y)}{(4-y)^2}= 0\\ &\\ &-2(4-y)+4 =0\\ &-8+2y + 4 = 0\\ &2y = 4\\ &y = 2\end{align}$$

y=2 si tiene sentido, es doblar a altura 2.

La esquina ira a parar a este punto X de abajo

x=sqrt(64-16y) = sqrt(32) = 4 sqrt(2) = 5.656854249

Y la doblez mínima mide

sqrt[(x^2+y^2)(1+64/x^2)] = sqrt[(32+4)(1+64/32)] = sqrt(36·3) = sqrt(48) = 4sqrt(3) = 6.92820323

Y eso es todo, espero que te sirva y lo hayas entendido. Si di algún paso muy largo o crees que falta algo pídeme que te lo explique.