Dibuja las regiones planas

Lo que seguramente conocerás es que la integral definida

$$\int_a^bf(t)dt$$

es el área limitada por el eje X dos rectas verticales x=a e y=b y una función f(t)

También sabrás que si F(t) es una función primitiva de f(t), es decir que

F '(t) = f(t)

entonces

$$Area = \int_a^bf(t)dt =F(b)-F(a)=x^3-x^2$$

Luego el área depende de dos valores a y b, como aquí solo nos dan el valor x haremos b=x y supondremos que a=0

Luego haremos

F(t) = t^3-t^2

con lo cual

F(x) - F(0) = x^3 -x^2 - 0^3 + 0^2 = x^3 - x^2

Luego ya sabemos como es F, y como f es la derivada tendremos

f(t) = F '(t) = (t^3-t^2)' = 3t^2 - 2t

Resumiendo.

x^3-x^2 es el área limitada por la función 3t^2-2t, el eje X, la recta t=0 y la recta t=x

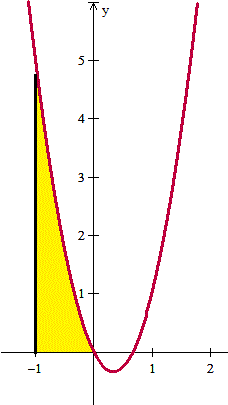
¡Bueno, espera! La integral definida ni es siempre el área. Es el área si entre los límites de integración la función es siempre positiva. O incluso es el área con signo negativo negativo si la función es negativa entre los límites, pero si la función cambia de signo es la suma de las áreas de las zonas positivas menos las negativas.

Entonces lo que hemos hecho de que x^3-x^2 sea el área entre 0 y x solo sirve para x<0

Si queremos que sirva para x>0 habría que hacer una simetría respecto del eje Y de la función f(t) = 3t^2-2t eso se hace haciendo

g(t) = f(-t) = 3(-t)^2 - 2(-t) = 3t^2 +2t

Entonces tendremos

x^3-x^2 es el área entre la función 3t^2 + 2t, el eje X y las rectas t=0 y t=x para x >=0

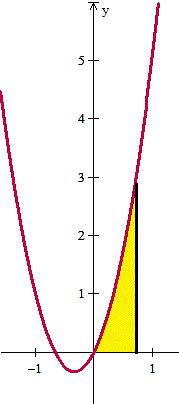
Y eso es todo.