Problemas de cadenas de markov

Algunos teoremas están extraídos de los apuntes de la UnADM, Procesos Estocásticos, Unidad 2, Cadenas de Markov a tiempo discreto.

Voy a hacer la gráfica.

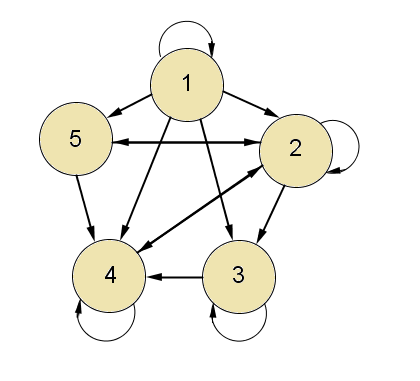
Del estado 1 se puede ir a todos pero desde nadie salvo el mismo se puede volver a 1, es un estado transitorio
Los estados 2, 3, 4 y 5 se comunican todos entre si y forman una clase

2-->3-->4 y 2--->5

3-->4-->2-->5

4-->2-->3 y 4-->2-->5

5-->4-->2-->3

Luego las clases de comunicación son: {1}, {2,3,4,5}

----------------

El periodo de la clase 1 es 1, puede comunicarse consigo mismo en 1 paso.
El 2 puede comunicarse consigo mismo en dos pasos
2-->4-->2
pero también en 3 pasos
2-->3-->4-->2
Luego su periodo es mcd(2,3)=1

Y como 2 está comunicado con 3,4 y 5 el periodo de estos estados por la proposición 3 de la pag 37 también es 1. Eso sirve para cadenas estacionarias, esta lo es ya que solo hay una matriz, si no habría varias. No obstante voy a comprobarlo porque la demostración de esa proposición es complicada y no me fío

Del 3 se vuelve en 3
3-->4-->2-->3
y en 5
3-->4-->2-->5-->2-->3
luego el periodo es mcd(3,5) = 1

Del 4 se vuelve en 2
4->2-->4
y se vuelve en 3
4-->2-->5-->4
Luego el periodo es mcd(2,3) = 1

Y del 5 se vuelve en 2
5-->2-->5
y se vuelve en 5
5-->2-->3-->4-->2-->5
luego el periodo es mcd(2,5) = 1
Luego resumiendo, todos los estados tienen periodo 1.

------------------------

La clase {1} es transitoria
La clase {2,3,4,5]} es recurrente

-----------------------

Llevamos la primera fila a la última subiendo todas un lugar
0 0.1 0.3 0.3 0.3
0 0 0.4 0.6 0
0 0.5 0 0.5 0
0 0.8 0 0.2 0
0.1 0.3 0.2 0.2 0.2

Ahora la primera columna a la última moviendo toas a la izquierda
0.1 0.3 0.3 0.3 | 0
0 0.4 0.6 0 | 0
0.5 0 0.5 0 | 0
0.8 0 0.2 0 | 0

------------------------------

0.3 0.2 0.2 0.2 | 0.1

Y eso es todo.