Calcula el volumen generado por las curvas dadas
Calcula el volumen generado por las curvas dadas alrededor del eje x
$$a) x=1+y^2, x=0, y=1, y=2$$
Tengo la respuesta
$$\int_3^{-1}2\pi y(1+y^2) dx = \frac{21\pi}{2}$$Pero me piden realizar un bosquejo de la región calculada
1 respuesta
La respuesta que dices no sé si estará bien, pero la integral esa no se corresponde con el área. Para empezar pones dx cuando sería en todo caso dy. Y si realizas la integral el resultado es -48pi.
No sé por qué extraño motivo cuando giran alrededor del eje y te dan funciones de x, y cuando giran alrededor del eje X te dan funciones de y. Con lo cal en todos los casos no te sirve la función que te dan y tienes que calcular la inversa. Me huele a mí que los enunciados están mal y donde dices giran en el eje X es el Y y viceversa, o que cuando te dan una f(x) te tendrían que dar una f(y) y viceversa.
Yo estoy haciendo los ejercicios de acuerdo a lo que dice estrictamente el enunciado, luego si el enunciado está mal, las respuestas estarán mal. De todas formas los dos que he hecho hasta ahora dan la misma respuesta que ponías, pero eso sí, la integral que plantean o planteas no es la qu resuelve el problema.
Y ahora tengo que ir a dormir a las 9 de mi país que ya está bien, este problema lo haré cuando me levante, que no veas el tiempo de lleva hacer esos dibujillos.
Puesto que gira respecto del eje X debemos poner la curva como función de x.
x=1+y^2
y^2= x-1
y = +- sqrt(x-1)
He variado la forma de hacer el dibujo, ne sé si será mejor o peor. En color está la superficie que genera el volumen al girar
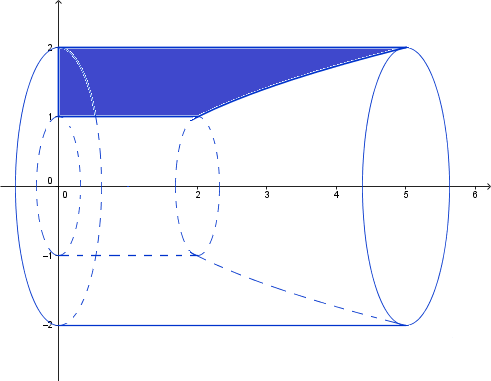
El volumen será el del cilindro exterior menos el cilindro interior que va de x=0 a x=2 y el hueco que genera la función y=sqrt(x-1) entre x=2 y x=5
El cilindro exterior mide
Pi·2^2·5 = 20pi
El cilindro interior entre x=0 y x= 2 mide
Pi·1^1·2 = 2Pi
el hueco que genera la función es
$$\begin{align}&\pi\int_a^b[f(x)]^2dx=\\ &\\ &\\ &\pi \int_2^5 (x-1)dx=\\ &\\ &\pi \left[\frac{x^2}{2}-x \right]_2^5=\pi\left(\frac{25}{2}-5-2+2\right)=\frac{15\pi}{2}\end{align}$$Luego el volumen de la pieza será
V = 20pi - 2pi - 15pi/2 = 18pi - 15pi/2 = 21pi/2
Ves lo que te decía. La solución del enunciado está bien, pero el método que se ha usado no lo está.
Y eso es todo.
