Representar la gráfica de una función de seno - coseno

Otros estudios previos serían la continuidad. Es continua siempre porque el denominador no se anula nunca. Tampoco hay ninguna asíntota. Es periódica con periodo 2pi. Los cortes con el eje X son los cortes del seno luego -pi, 0 y pi.

Otra cosa interesante es que tiene simetría central ya que

f(-x) = -f(x)

sen(-x) / (2-cos(-x)) = -senx / ( 2-cosx)

Y vamos ya con el crecimiento y extemos

Derivamos

f '(x) = [cosx(2-cosx) - senx·senx] / (2-cosx)^2 =

[2cosx - cos^2(x) -sen^(x)] / (2-cosx)^2 =

(2cosx -1) / (2-cosx)^2

Como el denominador es siempre positivo el signo de la derivada depende del signo del numerador. llamémoslo n(x) = 2cosx - 1

2cosx - 1 = 0

2cosx = 1

cosx = 1/2

En el intervalo [-pi, pi] las soluciones son -pi/3 y pi/3

Luego tenemos tres intervalos par estudiar el signo de la derivada

[-pi, -pi/3) tomamos n(-pi/2) = 2·0 -1=-1 <0 es decreciente

(-pi/3, pi/3) tomamos n(0) = 2·1 - 1 = 1 >0 es creciente

(pi/3, pi] tomamos n(pi/2) = 2·0 -1 = -1 <0 es decreciente

Y los estremos son

En -pi/3 cambia de decreciente a creciente, luego es un mínimo relativo

El valor de la función es

f(-pi/3)= sen(-pi/3) / (2 - cos(-pi/3)) = -[sqrt(3)/2] / (2 - 1/2) = -sqrt(3)/3

El punto del mínimo es (-pi/3 , -sqrt(3)/3

En pi/3 cambia creciente a decreciente, luego es un máximo relativo.

El valor de la función es

f(pi/3)= sen(pi/3) / (2 - cos(pi/3)) = [sqrt(3)/2] / (2 - 1/2) = sqrt(3)/3

El punto del máximo es (pi/3 , sqrt(3)/3)

Y con esto y algún punto más si se quiere hacerlo mejor se dibuja la curva.

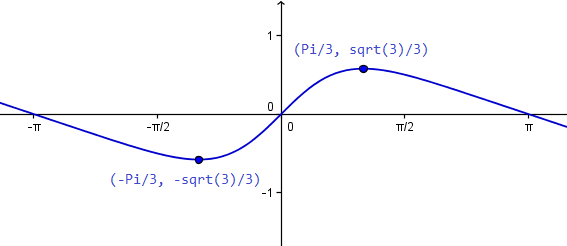
Y eso es todo.