Halla el área de la región acotada comprendida entre las gráficas de las funciones
$$y= \frac{1}{x^2+4}$$y
$$y= \frac{x}{16}$$en el eje OY
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
el enunciado es eso, el eje OY creo que es (0,y), supongo que hay que hallar el área que esta acotada entre (0,y) y esas dos funciones, de 0 a 2 en el eje de coordenadas seria una y de 2 a + infinito seria orea. Creo no estoy muy segura, espero que te sirva
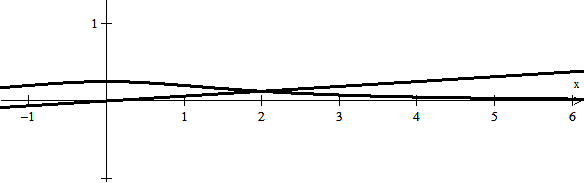
Voy a suponer que quieren decir el área entre esas curvas y el eje OY.
Entonces los límites en x son x=0 y x=2. Ya que es en x=2 donde se cortan, eso se puede comprobar numéricamente
1/(2^2+4) =1/8
2/16 = 1/8
La función que está por encima es la primera, la ponemos como minuendo y asi dará directamente positiva el área.
$$\begin{align}&Área=\int_0^2 \left(\frac{1}{x^2+4}-\frac{x}{16}\right)dx =\\ &\\ &\\ &\frac 14\int_0^2 \frac{dx}{1+\frac{x^2}{4}}-\left[ \frac{x^2}{32} \right]_0^2=\\ &\\ &\\ &\frac 14\int_0^2 \frac{dx}{1+\left(\frac{x}{2}\right)^2}-\frac 18=\\ &\\ &\\ &\frac 14·2\int_0^2 \frac{\frac 12dx}{1+\left(\frac{x}{2}\right)^2}-\frac 18=\\ &\\ &\frac 12\left[arctg \frac x2 \right]_0^2-\frac 18=\\ &\\ &\frac 12 arctg\,1 -\frac 18 =\frac{\pi-1}{8}\,u^2\end{align}$$Y eso es todo.
