Anónimo
Puede ayudarme con trigonometría y propiedades de polígonos. Gracias.
Demuestra que el apotema de un triángulo equilátero es equivalente a la mitad de su radio.
Demuestra que el perímetro de un triángulo equilátero circunscrito mide el doble del perímetro del triángulo equilátero inscrito en la misma circunferencia.
1 respuesta
Haremos el dibujo y todo irá sobre ruedas.
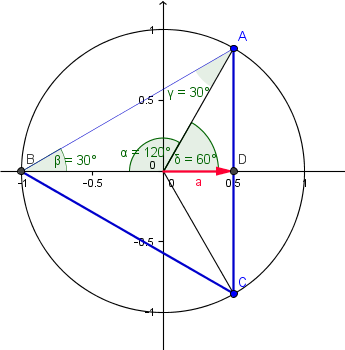
Cada ángulo del triángulo equilátero mide 60º. Lo situamos de modo que el eje X sea la bisectriz del ángulo en B. Asi el ángulo beta=30º. Como el triángulo ABO es isósceles al tener dos lados iguales al radio el ángulo gamma = 30º. Y entonces el angulo del triangulo que queda es alfa = 180º - 30º-30º = 120º
Y el ángulo delta es suplementario de alfa luego delta = 180º-º20º = 60º
Y el apotema es el radio por el cos(delta)
a = r·cos(60) = r/2
Ahora vamos con la parte segunda.
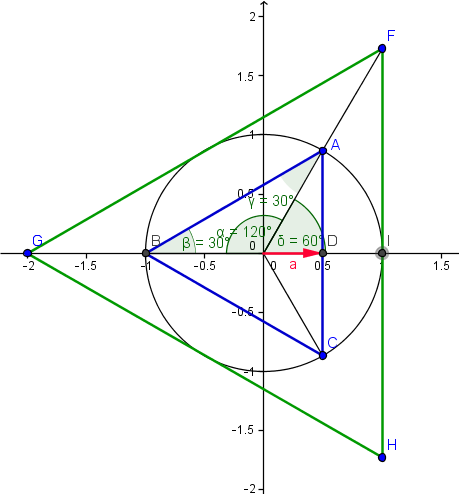
Hacemos el triángulo equilátero circunscrito que tiene lados paralelos al anterior. El lado FH debe ser tangente a la circunferencia luego el apotema del circunscrito es el doble del apotema del inscrito.
El segmento AD mide
AD = Rsen(60º) = 2asen(60º)
El segmento FI se puede hallar de la misma forma haciendo que el apotema valga el doble
FI = 4asen(60º)
Luego FI = 2·AD
Y el perímetro de ABD es 6·AD y el de FGHes 6FI = 12·AD
Luego el perímetro del circunscrito es el doble.
Y eso es todo.