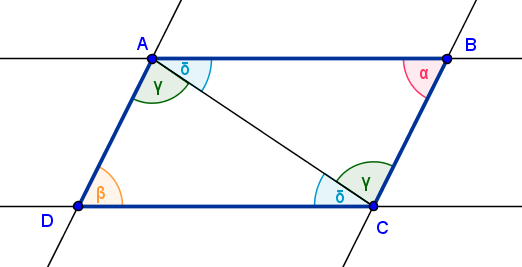
Sea el paralelogramo en forma de romboide definido por los puntos A, B, C
Sea el paralelogramo en forma de romboide definido por los puntos A, B, C y D. Un segmento de recta AC es una de las diagonales del romboide, entonces los ángulos de los vértices B y D son congruentes.
No lo demostré bien, ¿me ayudas?.
1 Respuesta
Hagamos el dibujo para entenderlo bien.
Lo que nos piden es demostrar que alfa = beta
Por ser un paralelogramo tendremos que las rectas que contienen los segmentos AB y DC son paralelas. Tomamos esas dos rectas cortadas por la secante AC, los dos ángulos marcados como delta son alternos internos, luego son iguales
Y por ser paralelogramo también son paralelas las rectas que contienen AD y BC. Tomamos la secante AC que las corta, entonces los ángulos gamma son alternos internos y por lo tanto iguales
Y ahora usaremos que la suma de los ángulos de un triángulo es 180º
En el triángulo ABC
alfa + gamma + delta = 180º
y en el triángulo ACD
beta + gamma + delta = 180º
igualando las ecuaciones
alfa + gamma + delta = beta + gamma + delta
y restando gamma y delta en ambos lados queda
alfa = beta
Y ya está.
