Problemas de regiones en el plano complejo

Amo 1965!

La parte real es la coordenada x del gráfico y la parte imaginaria es la coordenada y.

Luego el problema es equivalente a representar el conjunto

{(x,y) € R^2 | |x|<=|y+1|}

Si lo de dentro de un valor absoluto es positivo se puede quitar el valor absoluto dejándolo tal cual, y si es negativo debe cambiarse el signo de lo de dentro para quitarlo

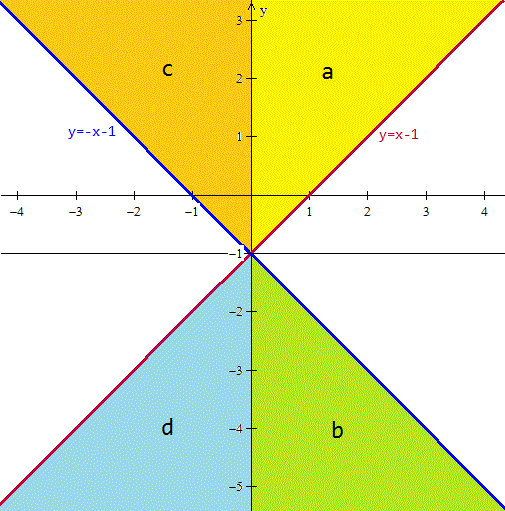
a) x <= y+1 , y >=x-1 , si x>=0, y>=-1 superior

b) x <= -y-1 , y <=-x-1 , si x >=0, y <-1 inferior

c) -x <= y+1 , y >= -x-1 , si x<0 , y>=-1 superior

d) -x <= -y-1 , y <= x-1 , si x<0, y <-1 inferior

Luego hay que dibujar las rectas

y = x-1

y = -x-1

Y tomar la zona superior a la recta correspondiente cuando la inecuación es y>= o la zona inferior cuando es y<=.

Esta es la gráfica, el conjunto es todo lo coloreado incluidas las lineas de frontera.

Y eso es todo.