Teorema de Gauss y ley de Gauss.
Resuelve la integral usando integral doble F dS, usando el teorema de la divergencia, Donde F(x, y, z) = (e^x)(y) + (xy+3) + (e^y)(x²), la región esta dada por el cilindro parabólico z = 1 - x², cortado por el plano z = 2 - y, y = 0
1 Respuesta
El teorema de la divergencia dice que el flujo de un campo vectorial F a través de una superficie cerrada S es igual a la integral de la divergencia extendida al volumen encerrado por esa superficie.
Y lo que tengo serios problemas es para escribir la fórmula porque cada libro tiene una notación distinta.
$$\begin{align}&Si \;F=X(x,y,z)\,i+Y(x,y,z)\,j+Z(x,y,z)\\ &\\ &\\ &div\,F= \frac{\partial X}{\partial x}+\frac{\partial Y}{\partial y}+\frac{\partial Z}{\partial z}\\ &\\ &\\ &\text{y entonces}\\ &\\ &\\ &\int\int\int_V div\,F\;dv=\int\int_S Fn \,ds\\ &\\ &\\ &\end{align}$$De acuerdo con eso la divergencia del campo vectorial del ejercicio es
div F = y·e^x + x + 0
Y los límites de la integral del volumen vamos a calcularlos.
Primero calculamos la intersección del cilindro con el plano
z=1-x^2
z= 2-y
1-x^2 = 2-y
y = 1+x^2
Bueno, será mejor hacer la gráfica, hay algo que no me concuerda.
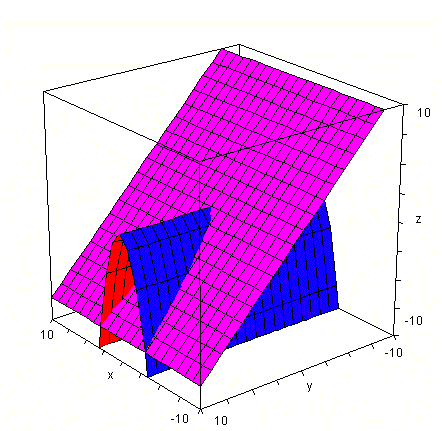
Este programa no es muy bueno ya que solo puede representar superficies z = f(x, y) con lo cual el plano y=0 no se puede dibujar, pero lo imaginamos, es uno vertical perpendicular a la linea de abajo donde pone y.
No sale ninguna superficie cerrada. Mira a ver el enunciado, seguramente falta de añadir el plano z=0 o darlo a entender de alguna manera.
Esta bien por favor tome el plano z=0 para que me apoye con la solución gracias.
Así si se forma una superficie cerrada como podrás intuir en la gráfica.
Pero la integral la haré mañana no está tan claro y aquí ya son las 8am tengo que ir a dormir.
Cortamos la superficie cerrada por planos paralelos al eje Z.
La variable z tomará valores entre 0 y el techo del cilindro z=1-x^2 que es z=1. Luego z varía entre 0 y 1.
Y los cortes son rectángulos, cuya anchura es 2 veces la coordenada x
z=1-x^2
x= sqrt(1-z)
Luego x variará entre -sqrt(1-z) y sqrt(1-z)
Y la longitud de los rectángulos va en disminución por el corte con el plano
z = 2-y
y = 2-z
luego y varía entre 0 y 2-z.
Luego la integral de F ds (o F·n ds según otros libros) usando el teorema de la divergencia es
$$\begin{align}&\int\int_S Fn \,ds=\int\int\int_V div\,F\;dv=\\ &\\ &\int_0^1\int_{-\sqrt{1-z}}^{\sqrt{1-z}}\int_0^{2-z} (ye^x+x)dy\,dx\,dz=\\ &\\ &\int_0^1\int_{-\sqrt{1-z}}^{\sqrt{1-z}}\left[\frac{y^2e^x}{2}+xy \right]_0^{2-z}dx\,dz=\\ &\\ &\int_0^1\int_{-\sqrt{1-z}}^{\sqrt{1-z}}\left(\frac{(2-z)^2e^x}{2}+x(2-z) \right)dx\,dz=\\ &\\ &\int_0^1\left[ \frac{(2-z)^2e^x}{2}+\frac{x^2(2-z)}{2} \right]_{-\sqrt{1-z}}^{\sqrt{1-z}}=\\ &\\ &\frac 12\int_0^1\left((2-z)^2(e^{\sqrt{1-z}}-e^{-\sqrt{1-z}})+(2-z)(1-z-1+z)\right)dz =\\ &\\ &\frac 12\int_0^1(2-z)^2(e^{\sqrt{1-z}}-e^{-\sqrt{1-z}})dz=\\ &\\ &t=\sqrt{1-z}\quad \\ &dt=-\frac{dz}{2 \sqrt{1-z}}\implies \\ &dz=-2 \sqrt{1-z}dt=-2tdt\\ &z=0\implies t=1\\ &z=1\implies t=0\\ &=-\int_1^0(1+1-z)^2(e^t-e^{-t})t\,dt=\\ &\int_0^1t(1+t^2)^2(e^t-e^{-t})dt=\\ &\\ &\int_0^1 (t+2t^3+t^5)e^tdt+\int_0^1(t+2t^3+t^5)e^{-t}dt=\\ &\end{align}$$Y esto se resuelve por partes, pero es bastante pesado de escribir sobre todo por que hay que hacerlo cinco veces y el ordenador ya no puede con tantas fórmulas escritas con el editor de ecuaciones. Escribo el resultado
$$\begin{align}&=\left[(t^5-5t^4+22t^3-66t^2+133t-133)e^t\right]_0^1+\\ &\left[(t^5+5t^4+22t^3+66t^2+133t+133)e^{-t}\right]_0^1=\\ &\\ &-48e+133 +360e^{-1}-133=\\ &\\ &-48e+360e^{-1}\approx 1.959071056\\ &\\ &\end{align}$$Y eso es todo. La integral está verificada , si acaso hay algo mal es antes de resolverla, en el planteamiento o en la elección de los límites de integración.
