Geometría, ejercicios de demostracion!
Encontrar tres formas diferentes de resolver el siguiente problema.
Es decir demostrar que el cuadrilátero B'A'ED es un paralelogramo.
1 Respuesta
¡Ah, también entiendo que el orden de construcción es este!
Primero se trazan las medianas. Luego el segmento B'A' y después los segmentos B'D y A'E que son paralelos a la mediana CC'. Finalmente se construye DE.
Debido a esta forma de construcción, unicamente quedaría demostrar que DE es paralelo a B'A'
Si no es esa la forma de construcción me lo dices. Que casi todos los ejercicios geométricos adolecen del orden de construcción y a veces no es nada obvio.
Lo de los tres métodos no puede ser. Yo no sé todo lo que estás estudiando para que haya nada más ni menos que tres métodos, si tuviera el libro quizá podría.
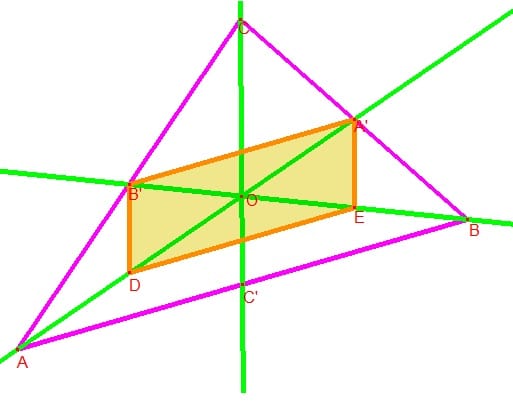
Los triángulos CAB y CB'A' son semejantes porque por la construcción de las medianas tenemos
CA/CB' = CB/CB' = 2
Luego B'A' es paralelo a AB y la mediana CC' también es mediana de triángulo CB'A'.
Añade el punto F como intersección de A'B' con CC' por que lo voy a utilizar.
A'F = B´F
o lo que es lo mismo
B'A' / B'F = 2
A'B' / A'F = 2
El triángulo B'OF es semejante a B'EA' por compartir un ángulo y ser paralelos los lados opuestos a ese ángulo. Luego
2 = B'A'/B'F = OF/EA'
El triángulo A'OF es semejante a A'DB' por compartir un ángulo y ser paralelos los lados opuestos a es ángulo. Luego
2 = A'B'/A'F = OF/DB'
Y juntando esta igualdad con la de poco más arriba tenemos
OF/ EA' = OF / DB'
Luego EA' = DB'
Es decir que esos dos lados miden lo mismo y son paralelos, entonces a DE no le queda otro remedio que ser paralelo a A'B'.
Y eso es todo espero que te sirva y lo hayas entendido. Si no consúltame. DE los miles de teoremas de geometría no me acuerdo de casi ninguno pero algo si puedo hacer.
el enunciado del problema es; EN UN TRIANGULO ABC LAS MEDIANAS AA',BB',CC' SE ENCUENTRAN EN O. se toma D punto medio de OA, E punto medio de BO.
con respecto a la construcción que me describes; si primero construyo el triangulo ABC, luego el segmento B'A' , luego los puntos medios de AO y BO que son D y E respectivamente.
pues para la demostración había pensado en una forma me guio del libro GEOMETRÍA DE CLEMENS, dice que por el teorema de punto medio pag 276, dice:
TEOREMA DEL SEGMENTO MEDIO, el segmento que une los puntos medios de dos lados de un triangulo es paralelo al tercer lado y tiene la mitad de su longitud.
Si, ese teorema se deduce fácilmente de las semejanzas con proporción 2 a 1 de triángulos que se forman, usando el teorema de Thales.
La construcción que yo suponía tenía otro orden pero la figura resultante es la misma. Usando ese teorema sobre ABC y sobre ABO tienes los segmentos B'A' y DE que miden ambos la mitad de AB y ambos paralelos a AB luego paralelos entre sí. Y entonces los otros dos lados que completan el cuadrilátero son paralelos y miden lo mismo y se forma el paralelogramo.
