Círculos en un Rectangulo

Pes la verdad es que el problema es complicado ya que depende mucho de el radio del cilindro y el área de la caja puede que te convenga mas una cosa o otra.

Por ejemplo el caso que expones donde la caja mide 32x23 cm y el cilindro 6.5.

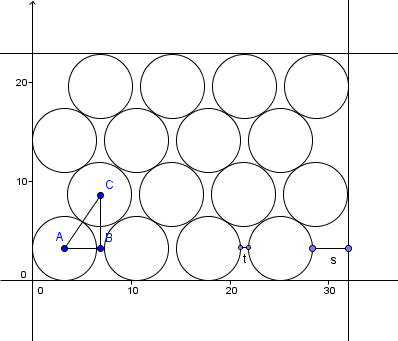
En este caso si colocas los cilindros de forma lineal quedaría así:

$$\begin{align}&\text{32 de largo y 23 de ancho entonces si dividimos}\\ &\\ &\frac{32}{6.5}=4 \text{ y nos sobran 6 cm (no cabe otro cilindro)}\\ &\text{}\\ &\frac{23}{6.5}=3 \text{ y nos sobran 3.5 cm (no cabe otro cilindro)} \\ &\end{align}$$

Nota: Si te cuesta trabajo sacar lo que sobra se saca haciendo la división y la parte decimal la multiplicas por el 6.5 que es entre lo que la estas dividiendo. Ej. 32/6.5=4.923076923076923, 4 es la parte entera y 0.923076923076923*6.5=6 que son los centímetros que te sobran.

Entonces te cabrían 12 cilindros (3 a lo ancho x4 a lo largo).

Para saber cuanto desperdicias sacas el área de los cilindros y el área de la caja.

$$\begin{align}&cilindros=\pi*diametro=\pi*6.5=20.42\\ &20.42*12cilindros=245.04\\ &caja=lado*lado=32*23=736\\ &736-245.04=490.96\end{align}$$

Estarias desperdiciando 490.96.

Pero si en la fila de 4 cilindros te sobran 3.5cm entonces si distribuyes esa fila tendrias 3 separaciones de aproximadamente 3.5/3espacios = 1.1667cm.

(Para esto tendría que mandarte un dibujo pero ahorita no tengo como mandártelo)

Pero el chiste de esto es que al poner un cilindro entre estos espacios se forma un triangulo entre sus centros (imaginatelo es el que queda en medio y los dos que quedan al lado)

Es un triangulo de base 3.25 de un radio y 3.25 del otro mas 1.1667 del espacio es igual a

7.6667cm de base y otros dos lados de 6.5(la suma de los 2 radios).

Podríamos formar un triangulo rectángulo de 3.8333 de base(7.66667/2) hipotenusa de 6.5 (que es la suma de los 2 radios) y por teorema de pitagoras:

$$\begin{align}&h=\sqrt{c^2+c^2}\\ &despejando\\ &c=\sqrt{h^2-c^2}\\ &c=\sqrt{6.5^2-3.8333^2}=5.25\end{align}$$

Los 5.25 es el espacio que ahorras en vez de los 6.5.

Esto lo multiplicas por 3 que son los espacios que tienen esta medida serian 15.75 mas 6.5 (que es la suma de los dos radios de la orilla que son de 3.25) y nos da 22.25 que quiere decir que si cabe la lo ancho que es de 23.

Con este acomodo de cabrían 15 cilindros que son 3 mas de los que te cabrían con el otro acomodo.

Notese que si la caja midiera 22 de ancho solo nos cabrían 11 cilindros y nos convendría mas el otro acomodo, así que por eso comento que depende de la caja y del cilindro que acomodo ocuparías.

Seria mejor que te lo pudiera explicar con imagenes no se si quieras que te apoye con una video conferencia o por algun otro medio. Tembién podria realizarte algún programita que te ayude a decidir.

¿Quieres decir que los cilindros se pueden poner de forma que el de arriba pueda meterse algo entre los de abajo?

En principio haciendo la división entera de la longitud y altura y entre el diámetro obtenemos dos números cuyo producto nos dice una cantidad de cilindros que caben seguro. Pero llevándolos algunos a la derecha y otros a la izquierda se puede conseguir que quepan más.

Mi opinión es que lo mejor sería hacer las cajas justas, es decir que la longitud y altura fuese múltiplo del diámetro, y si fuesen cajas cuadradas aun mejor.

El cálculo en otros casos no es sencillo, se hace mucho más rapido probando en la caja que haciendo cuentas aparte. Habrá casos en que lo mejor sea formar filas todas con el mismo número de cilindros y otros en que un fila tenga un cilindro menos que las de arriba y abajo y otros más raros todavía.

En este caso concreto

32 / 6.5 = 4.923

23 / 6.5 = 3.53846

En formación militar solo cabrían 4 · 3 = 12

Pero el que falte poco para caber 5 cilindros a lo largo y que también sobren 0.53846 cilindros en altura nos da esperanzas de que quepan más. No costaría mucho probar que se pueden poner 3 filas de 5 con uno un poquito más levantado que los demás. Eso serían 15 cilindros. Pero vamos a ver que caben 16 con esta formación

El dibujo sugiere que caben, pero hay que demostrarlo. Lo haré de forma que las filas queden rectas. Los huecos entre circunferencias son tres de longitud t y uno de longitud s. Y el hueco que hay es 32 - 4·6.5 = 32-26 = 6

Luego tendremos

3t + s = 6

Para que la circunferencia de la derecha de la segunda fila esté a la misma altura que las otras el triángulo que se forme debe ser igual que el ABC. Entonces el lado equivalente a la base AB será

3.25 del radio de la de abajo derecha + s - 3.25 del radio de la de arriba = s

Como

AB = 3.25 + t/2

tenemos

s= 3.25+ t/2

Si llevamos este valor a la de arriba tenemos

3t + 3.25 + t/2 = 6

7t/2 = 2.75

t = 2.75 · 2 / 7 = 5.5/7 = 11/14

AB = s = 6-3t = 6 - 33/14 = 51/14

AC = diámetro = 6.5

Por el teorema de Pitágoras

BC= sqrt[6.5^2 - (51/14)^2] = 5.383269623

Entonces la altura a la que se sitúa la segunda fila es

3.25 + 5.383269623 + 3.25 = 11.88326962

La primera fila proporciona 6.25 de altura y cada fila extra 5.383269623

Luego la altura de la 4 fila será

6.25 + 3 · 5.383269623 = 22.39980887

Que es menor que 23, luego caben 4 filas de 4 y caben 16 cilindros.

Pero no siempre será este el modelo a usar, por eso no es fácil.

Y eso es todo.

Muchísimas gracias por tu pronta respuesta, lo probare este fin de semana, y si tengo alguna duda, te preguntare.

Nuevamente, muchas gracias, llevo mucho tiempo con este asunto y en 5 minutos, solucionado.

Un abrazo,

David

Hola Valero,

Lo he estado viendo, y uffff, por eso me suspendían en matemáticas, ja ja, si no te molesto mucho, me podrías mandar una Excel, con lo anterior, y asi lo comprenderé mejor, y asi compruebo con otras medidas.

Te debo una caña, mi email es [email protected]

Gracias nuevamente,

David